![Oberflaechenbehandlung vergoldet]()
Druckfedern, teilweise auch Zugfedern und Schenkelfedern erhalten durch eine nachträgliche Behandlung ihrer Oberflächen zusätzliche Eigenschaften – sie werden je nach Anwendungsfall beispielsweise härter, rost- oder wärmebeständiger. Gutekunst Federn bietet für seine Katalog- und individuellen Stahlfedern neben klassischen Verfahren wie Glanzverzinken, Brünieren, Elektropolieren, Beizen, Phosphatieren, Passivieren, Verchromen, Vernickeln, Verzinken und Kugelstrahlen auch eine Vielzahl von speziellen Oberflächenbehandlungen. Dazu zählen Dickschicht-Passivierungen, Pulverbeschichtungen, Delta®-Tone und Delta®-Seal Korrosionsschutzsysteme, Glasperlenstrahlen, PTFE-Teflonbeschichtungen, Vergolden, Verkupfern oder auch das Chromatieren von verzinkten Stahlfedern.
Alle Oberflächenbehandlungen für Sie im Überblick:
Klassische Oberflächenbehandlungen für Stahlfedern
Brünieren
Hauptmerkmale: Das Brünieren ist eine optische Oberflächenbehandlung. Durch das Verfahren weisen die Stahlfedern eine gleichmäßige Farbe auf, sind aber nur gering korrosionsbeständig.
Das Brünieren zählt zu den klassischen Oberflächenbehandlungen und ist ein nicht schichtbildendes Verfahren, bei dem Sauerstoff in die äußerste Schicht eingelagert wird. Durch die Behandlung bildet sich auf einem niedrig legierten Eisenwerkstoff wie der Stahlfeder ein schwarzer, dünner und nichtmetallischer Überzug aus Eisenoxid. Dieser meist weniger als ein Mikrometer dicke Belag wertet das Material nicht nur optisch auf, sondern schützt es auch. Der Vorgang erfolgt bei niedrigen Temperaturen unter 150 Grad Celsius. Dadurch entsteht keine thermische Belastung. Struktur und Rautiefe der Feder werden dabei nur unwesentlich verändert. Die Maßhaltigkeit der beschichteten Werkstücke bleibt gleich.
Elektropolieren
Hauptmerkmale: Das Elektropolieren behandelt die Oberflächen von Edelstahl. Es dient vor allem dazu, das Material optisch zu veredeln – beispielsweise bei medizinischen Geräten.
Das Elektropolieren besteht aus einem einzigen Arbeitsgang, bei dem mittels einer anodischen Auflösung eine sehr dünne Schicht der Oberfläche abgetragen wird. Verunreinigungen, Partikel, Mikrorisse sowie Gefügestörungen und lokale Spannungen werden ebenfalls bereinigt. Die behandelten Oberflächen zeichnen sich durch verschiedene Eigenschaften aus: Sie sind metallisch rein und glänzend, grat- und partikelfrei, im Mikrobereich geschlossen und verfügen über optimale Eigenschaften des Grundwerkstoffes. Ein weiterer Vorteil: Das Verfahren ist besonders schonend, und die Stahlfeder wird weder thermisch noch mechanisch belastet.
Vorteile gegenüber anderen Verfahren sind auch die gute Korrosionsbeständigkeit, minimierte Mikrorauheit, verbesserte Dauerfestigkeit sowie ein reduzierter Reibungskoeffizient. Behandelte Oberflächen überzeugen zudem durch eine geringe Produktanhaftung sowie eine verringerte Belagbildung. Sie lassen sich somit sehr leicht und schnell reinigen. Das Anwendungsgebiet reicht von der Chemie- und Pharmaindustrie über Umwelttechnik und Elektronikindustrie bis hin zur Architektur und Baubranche.
Beizen
Hauptmerkmale: Das Beizverfahren entfernt auf chemischen Weg alle Verunreinigungen einer Oberfläche.
Beizen ist ein Verfahren, das alle Verunreinigungen von Edelstahloberflächen auf chemischen Weg – sprich durch Säure – beseitigt. Das Ergebnis ist eine metallisch reine Oberfläche der Metallfeder. Nur darauf kann sich in einem nächsten Schritt die schützende Passivschicht bilden.
Glanzverzinken
Hauptmerkmale: Dieses Verfahren zählt zu den optischen Oberflächenbehandlungen und bietet einen hohen Korrosionsschutz.
Das Glanzverzinken ist ein galvanisch erzeugtes Schutz-System für Stahloberflächen. Bei dem Vorgang entsteht eine sehr dünne Zinkmetallschicht. Um das Metall hinreichend vor Korrosion zu schützen, wird die Schicht zudem passiviert oder chromatisiert. Damit wird das Material deutlich beständiger. Korrosionsspuren, auch als Weißrost bekannt, lassen sich mit dem Glanzverzinken verhindern. Das bearbeitete Material ist zudem haftfester, thermisch beständiger, überzeugt durch eine hohe Funktionalität und sieht ansprechender aus.
Phosphatieren
Hauptmerkmale: Das Besondere beim Phosphatieren sind der temporäre Korrosionsschutz und die günstigen Gleiteigenschaften.
Das Phosphatieren, auch Bondern, Atramentieren oder Parkerisieren genannt, zählt zu den häufigsten Verfahrenstechniken bei der Oberflächenbehandlung von Stahlfedern. Hierbei wird mittels chemischer Reaktionen der metallischen Oberfläche mit einer Phosphat-Lösung eine Konversionsschicht aus fest haftenden Metallphosphaten gebildet. Diese Oberflächen sind für Anwendungen interessant, bei denen Wert auf einen temporären Korrosionsschutz, eine gute Haftvermittlung für nachfolgende Lackierungen, eine Reib- und Schleißverminderung oder auch auf die elektrische Isolation gelegt wird. Das Phosphatieren ist zudem sehr wirtschaftlich und kostengünstig.
Passivieren
Hauptmerkmale: Passivierte Oberflächen verfügen durch ihre Oxidschicht über eine hohe Beständigkeit, können sich selbst regenerieren und bieten einen guten Korrosionsschutz.
Beim Passivieren entsteht auf der Stahlfeder eine Schutzschicht, die sogenannte Passivschicht. Diese Schutzschicht kann durch Passivierungschemikalien oder aber auch natürlich durch Feuchtigkeit und Sauerstoff entstehen. Dieser Überzug verhindert Korrosion – oder kann sie zumindest beträchtlich verlangsamen. Für dieses Verfahren müssen die Oberflächen metallisch rein sein. Das natürliche Passivieren dauert mehrere Tage. Kommen Passivierungschemikalien zum Einsatz, reduziert sich die Zeit auf wenige Minuten.
Verchromen
Hauptmerkmale: Das Verchromen ist eine optische Oberflächenbehandlung und bietet einen guten Korrosionsschutz.
Verchromte Oberflächen sind mehrschichtig aufgebaut. Sie schützen die Metallfedern vor Korrosion und weisen eine geringe Haftreibung auf. Sie können mechanisch nachbearbeitet werden, sind auch bei hohen Temperaturen beständig und laufen nicht an. Verchromte Oberflächen finden branchenübergreifend in vielen Bereichen der technischen Industrie Anwendung.
Vernickeln
Hauptmerkmale: Vernickelte Oberflächen sind zum einen korrosionsbeständig und weisen zum anderen günstige Gleiteigenschaften auf. Vernickeln zählt zu den optischen Oberflächenbehandlungen.
Nickel eignet sich für eine Vielzahl von unterschiedlichen Anwendungen und gehört zu galvanischen Metallüberzügen. Um Stahlfedern zu vernickeln, werden diese nach einer speziellen Vorbehandlung in einen Nickelelektrolyten – eine nickelsalzhaltige, wässrige Lösung – eingetaucht. Durch das Anlegen einer elektrischen Spannung bildet sich auf der Oberfläche der Feder eine feine Schicht. Der Überzug ist sowohl gegen Luft und Wasser als auch verdünnte Säuren und einige Laugen resistent. Ungeeignet ist Nickel dagegen im Kontakt mit Salpetersäure, konzentrierten Salzsäuren und Ammoniak. Das Übergangsmetall weist eine silberhelle Farbe mit einem leicht gelblichen Farbton auf. Durch seine charakteristische Färbung unterscheidet es sich sehr gut von verchromten Oberflächen. Nickel ist allerdings unbeständig gegen Anlaufen und kann mit der Zeit eine dunkle Färbung annehmen.
Verzinken
Hauptmerkmale: Verzinkte Oberflächen bieten einen besonders guten Korrosionsschutz.
Beim Verzinken werden Stahlfedern mit einem metallischen Überzug aus Zink versehen. Häufige Verfahren sind das kontinuierliche und das diskontinuierliche Feuerverzinken, thermisches Spritzen mit Zink sowie das galvanische Verzinken. Die Verfahren unterscheiden sich zum einen durch die Herstellung der Schutzschicht sowie durch ihre Schichtdicke. Von dieser hängen auch die Schutzdauer und die mechanische Belastbarkeit des Werkstückes ab.
Neben seiner abschirmenden Wirkung ist Zink korrosionsbeständig. Verzinkte Werkstücke werden häufig als Opferanode gegen Kontaktkorrosionen verwendet. Damit eignen sie sich für Anwendungen, bei denen edlere Metalle mit unterschiedlichem Lösungspotenzial leitend verbunden sind. Der verzinkte Werkstoff verhindert hier bis zu einem Abstand von fünf Millimetern die Korrosion der Metalle. Freiliegende Schnittkanten und Fehlstellen im Zinküberzug lassen sich so optimal schützen.
Kugelstrahlen
Hauptmerkmale: Das Kugelstrahlen erhöht die dynamische Lebensdauer von Stahlfedern deutlich.
Das Kugelstrahlen ist eine besondere Art der Oberflächenbearbeitung. Pressluft oder Schleuderräder schießen bei diesem Verfahren das Strahlmittel mit hoher Geschwindigkeit auf die Federn. Das Strahlmittel besteht aus runden oder gerundeten Körnern, die dem Vorgang seinen Namen geben.
Ziel des Kugelstrahlens ist es, das Oberflächenvolumen des Werkstoffs zu vergrößern und eine Druckeigenspannung zu erzeugen. Die Folge ist eine Verdichtung des Werkstoffs und damit die Verfestigung der Oberfläche. Bei diesem Verfahren wird die Dauerfestigkeit der Metallfeder deutlich verbessert.
Spezielle Oberflächenbehandlungen für Stahlfedern
Dickschicht-Passivieren
Hauptmerkmale: Durch das Dickschicht-Passivieren entsteht eine klare irisierende Oberfläche, die einen guten Korrosionsschutz bietet.
Das Verfahren wird auch als Transparentpassivierung bezeichnet. Hierbei wird eine nichtmetallische Schutzschicht auf einem metallischen Stoff wie einer Stahlfeder erzeugt. Der Überzug ist absolut Chrom-VI frei und kommt vor allem dort zum Einsatz, wo herkömmliche Chromatierungen nicht verwendet werden dürfen. Diese Art der Oberflächenbehandlung ist sehr gut für höhere Beschichtungen geeignet.
Pulverbeschichten
Hauptmerkmale: Das Pulverbeschichten zählt ebenfalls zu den optischen Oberflächenbehandlungen. Pulverbeschichtete Materialien besitzen eine hervorragende Glanzhaltbarkeit und Farbechtheit der 180 verschiedenen RAL-Farben.
Um Stahlfedern so zu bearbeiten, wird das entsprechende Farbpulver elektrostatisch aufgeladen und mithilfe einer sogenannten Pulverpistole auf das Material aufgebracht. Die Pulverlacke basieren auf diversen Bindemitteln wie Acrylat-, Epoxid- und Polyesterharz. Sie werden in allen RAL-Farben und in jedem gewünschten Zwischenton angeboten. Einzige Voraussetzung: Die Feder muss elektrisch leitfähig sein. Dies trifft zu, wenn sie beispielsweise aus Stahl oder Aluminium gefertigt ist. Anschließend wird das Pulver bei Temperaturen zwischen 140 und 200 Grad Celsius in einem Ofen in den Werkstoff gebrannt. Das erzeugt eine gleichmäßig dichte Beschichtung. Diese überzeugt durch eine hohe Licht- und Wetterbeständigkeit und ist zudem stoß- und kratzfest.
Delta®-Tone und Delta®-Seal-Beschichtung
Hauptmerkmale: Das Delta® Mikroschicht-Korrosionsschutz-System besteht aus einem zweischichtigen Aufbau. Delta-Tone ist die Grundbeschichtung (Basecoat), Delta-Seal die anschließende Deckbeschichtung (Topcoat). Beide zusammen bilden einen sehr hohen Korrosionsschutz für Metallfedern.
Durch den Aufbau aus Grund- und Deckbeschichtung können maßgeschneiderte Lösungen in Bezug auf die Funktionseigenschaften, das Reibverhalten und die Korrosionsbeständigkeit von Oberflächen erreicht werden.
Delta®-Tone (Basecoat)
Beim Delta®-Tone-Verfahren wird eine anorganische und mikroschichtbildende Grundschicht auf die Stahlfedern aufgebracht, die Zink- und Aluminiumlamellen enthält. Durch den anschließenden Einbrennprozess entsteht ein silbermetallisch glänzender Überzug mit gleichmäßiger Dicke. Dieser weist hervorragende Korrosionsschutzeigenschaften auf und stellt gleichzeitig eine sehr gute elektrische Leitfähigkeit sicher. Dies ermöglicht einen kathodischen Schutz und bannt die Gefahr einer Wasserstoffversprödung.
Je nach Anforderung der passende Basecoat:
- Delta®-Tone 9000 eignet sich speziell für Federn, Federbandschellen und Stanz-Biegeteile.
- Delta-Protekt® KL 100 wurde gezielt für Gewindeteile entwickelt und wird häufig in der Automotivebranche eingesetzt. Die Grundschicht hält Dauertemperaturbelastungen von 96 Stunden bei 180 Grad Celsius stand.
- Delta-Protekt® KL 105 macht mit integriertem Schmiermittel den Einsatz eines Topcoats überflüssig. Die Beschichtung ist auf die spezifische Reibungszahl eingestellt und ermöglicht somit als 2-in1-System Kosteneinsparungen.
- Delta-Protekt® KL 130 ist dunkelgrau und als Untergrund für schwarze Decktöne prädestiniert, weil Schlagstellen nicht mehr sichtbar sind.
- Delta-Protekt® KL 120 eignet sich besonders bei Verbindungselementen mit Gewinden und für Federn oder Federbandschellen. Die Rot- und Weißkorrosionsbeständigkeit geht weit über die Anforderungen anderer Oberflächenveredelungen hinaus.
Delta®-Seal (Topcoat)
Delta®-Seal ist eine Deckbeschichtung aus organisch hoch vernetztem, mikroschichtbildendem Material. Sie ergänzt optimal die zuvor angebrachte Grundschicht. Das Beschichtungs- und Einbrennverfahren hinterlässt einen haftfesten, chemikalienresistenten Belag. Eine hervorragende Beständigkeit gegen äußere Einflüsse wird durch den Einsatz bestimmter Harze wie Acrylat-, Epoxid- und Polyurethanharz mit einer angepassten Aushärtung erreicht.
Die Delta®-Seal Varianten, die schwarzen Delta-Protekt® VL 450 oder Delta-Protekt® VT 600 sowie das silberne Delta-Protekt® VL 411 GZ.
Glasperlenstrahlen
Hauptmerkmale: Das Glasperlenstrahlen ist eine spezielle Form des Kugelstrahlens.
Beim Glasperlenstrahlen schleudern Druckluft-, Schleuderrad- oder Injektorstrahlanlagen sehr kleine Glasperlen mit einer hohen Geschwindigkeit gegen die Oberfläche der Stahlfeder. Durch den Prozess entstehen sehr homogene Oberflächen mit hervorragenden optischen Eigenschaften. Glasperlenstrahlen wird daher zur eisenfreien Reinigung und für dekorative Oberflächen eingesetzt.
Teflonbeschichten (PTFE)
Hauptmerkmale: Teflonbeschichtete Stahlfedern weisen sehr gute Gleiteigenschaften auf.
Beschichtungen aus Teflon, auch PTFE (Polytetrafluorethylen) genannt, verfügen über verschiedene Eigenschaften: Dazu gehören neben einer sehr guten Korrosionsbeständigkeit und optimalen Antihaftfähigkeiten auch niedrige Reibungskoeffizienten sowie die Resistenz gegen hohe Temperaturen. Zum Einsatz kommen sie unter anderem in der Lebensmittelbranche, bei Reinraumanwendungen, in der Textil- und Papierindustrie sowie im Anlagen- und Maschinenbau.
Vergolden
Hauptmerkmale: Das Vergolden zählt ebenfalls zu den optischen Oberflächenbehandlungen. Vergoldete Materialien sind nicht nur besonders leitfähig, sie verhindert auch einen zu großen Schaltfunken. Mechanisch und chemisch sind sie jedoch wenig widerstandsfähig.
Beim chemischen Vergolden wird die Stahlfeder mit einer dünnen Schicht aus reinem Gold überzogen. Damit bleibt die Lötbarkeit des Werkstoffes erhalten und wird noch verbessert. Zum Einsatz kommen vergoldete Metallfedern deswegen vorzugsweise in der Elektroindustrie. Zu den Anwendungsgebieten zählen aber auch dekorative Bereiche.
Verkupfern
Hauptmerkmale: Verkupferte Metallfedern sind zum einen korrosionsbeständig und zeichnen sich zum anderen durch eine gute Leitfähigkeit aus.
Beim Verkupfern überzieht eine dünne Schicht aus Kupfer die metallischen Federn. Dieser Überzug ist eine beliebte Grundlage für viele Korrosionsschutzsysteme – unter anderem für Nickel- oder Chrombeläge. Denn der Belag sorgt für einen dauerhaften Schutz. Die Schicht beträgt in der Regel 5-15 µm. Verkupferte Federn bieten auch eine verbesserte thermische und elektrische Leitfähigkeit. Ein weiterer Vorteil: Sie können problemlos lackiert werden.
Verzinkt Chromatieren
Hauptmerkmale: Das Chromatieren verzinkter Bauteile bildet eine funktionelle und optische Oberflächenbehandlung. Sie bietet einen hohen Korrosionsschutz und ist in den Farben Blau, Gelb, Schwarz und Oliv erhältlich.
Vor dem Chromatieren müssen die Stahlfedern galvanisch verzinkt werden. Erst im nächsten Schritt tauchen sie in eine Lösung aus Chromsäure und verschiedenen Zusatzstoffen. Hierbei bildet sich eine sehr dünne chemische Umwandlungsschicht, auch Konversionsschicht genannt – ohne das Anlegen einer elektrischen Spannung. Die verschiedenen Chromatierungsarten lassen sich nach Farben unterschieden. Möglich sind Blau, Gelb, Schwarz und Oliv. Die Farbe Blau ist RoHS-konform und damit Cr(VI)-frei. RoHS steht für Restriction of Hazardous Substances, also die Beschränkung der Verwendung bestimmter gefährlicher Stoffe. Alle anderen Farben entsprechen nicht dieser Richtlinie und eignen sich damit beispielsweise auch nicht in Branchen wie der Automobilindustrie.
Eine gute Alternative zu Chrom (VI)-Oberflächen sind Dickschicht-Passivierungen. Bei diesem Verfahren entsteht eine klare irisierende Oberfläche mit einem guten Korrosionsschutz.
Folgende Farben und Eigenschaften werden verzinkt-chromatiert angeboten:
- Blau: Der Farbton geht leicht ins Bläuliche. Es besteht meist ein fließender Übergang zum Transparenten hin. Der Korrosionsschutz chromatierter blauer Oberflächen ist relativ schwach, die Schicht allerdings aber Cr (VI)-frei und damit konform nach der Richtlinie RoHS 2002/95/EG.
- Gelb: Die Färbung ähnelt Messing oder einem unreinen Goldton. Diese Art der Chromatierung sorgt für einen optimalen Korrosionsschutz und kommt häufig zum Einsatz. Die Schicht ist Chrom (VI)-haltig und nicht RoHS-konform.
- Schwarz: Bei dieser Kolorierung bleibt der Metallcharakter der Oberfläche stellenweise erhalten. Denn der Farbton ist nicht so kräftig wie bei einer Lackierung. Der Korrosionsschutz der Schicht ist mittel bis gut. Die Beschichtung ist Chrom (VI)-haltig und nicht RoHS-konform.
- Oliv: Die Farbe Oliv ist sehr kräftig, wodurch der Metallcharakter der Oberschicht größtenteils verloren geht. Auch diese Schicht ist Chrom (VI)-haltig und damit nicht RoHS-konform.
Sie möchten nähere Informationen zu Oberflächenbehandlungen für Druckfedern, Zugfedern und Schenkelfedern? Die Technikabteilung von Gutekunst Federn erreichen Sie telefonisch unter (+49) 035877 227-11 oder per E-Mail an service@gutekunst-co.com.
Weitere Informationen:
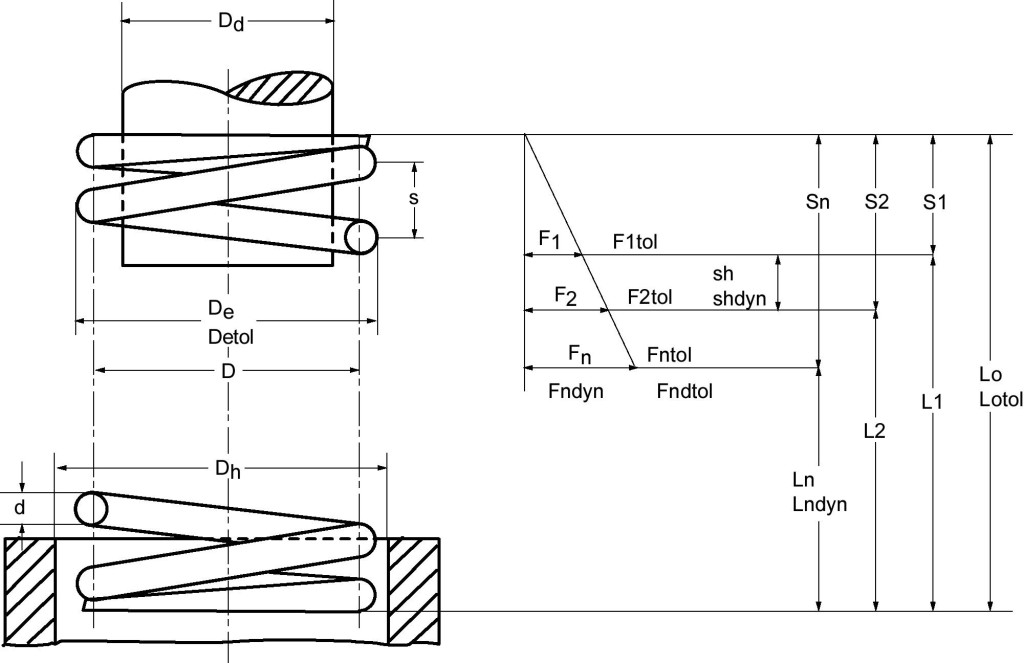
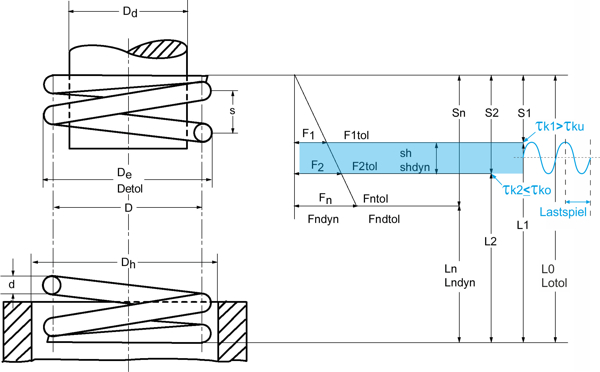
Der 
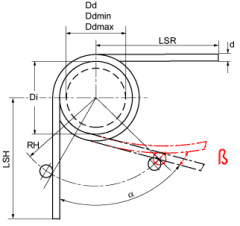
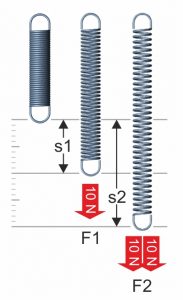
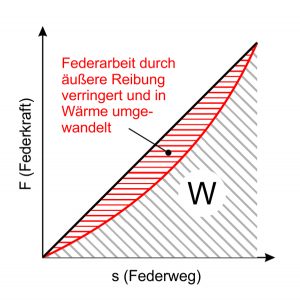
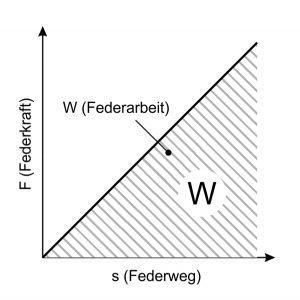Technische Federn sind auch heute noch eines der wichtigsten Maschinenelemente und werden in Fahrzeugen, feinmechanischen oder elektrotechnischen Apparaten, medizinischen Geräten, Haushaltgeräten u.v.m. erfolgreich eingesetzt. Häufig hängt vom störungsfreien Arbeiten der Metallfeder die Funktion des gesamten Geräts oder Maschinenteils ab.
