Bei der Mischschaltung werden mehrere Federn parallel und hintereinander geschaltet. So ergibt sich für die Gesamtfederrate folgende Formel:

Gesamtfederrate:
Bei der Mischschaltung werden mehrere Federn parallel und hintereinander geschaltet. So ergibt sich für die Gesamtfederrate folgende Formel:

Gesamtfederrate:
Die Federkennlinie zeigt, wie die Metallfeder sich bei der Arbeit verhält. Sie beschreibt das Verhältnis zwischen Federkraft (F) und Federweg (s). Je nach Bauform der Feder oder eingesetztem Federsystem unterscheidet man in eine lineare (b), progressive (a), degressive (c), bzw. kombinierte Federkennlinie.
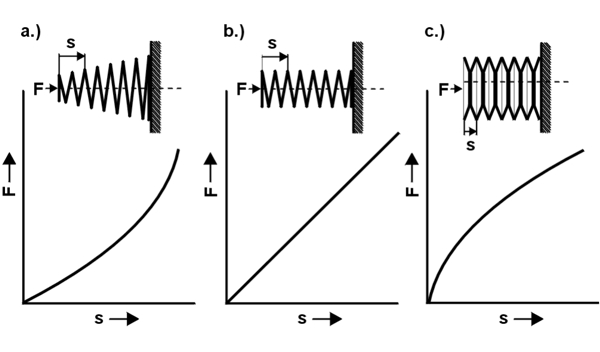
Eine Progressive Federkennlinie (a), die mit Zunahme der Einfederung die Kraft erhöht, erhält man mit einer konischen Federbauform und mit einer Mischschaltung von Einzelfedern. Eine lineare Federkennlinie (b), die mit Zunahme der Einfederung die Kraft gleichmäßig abgibt, erhält man mit einer zylindrischen Bauform und mit einer Reihen- oder Parallelschaltung. Eine degressive Federkennlinie (c), die mit Zunahme der Einfederung die Kraft verringert, erreicht man mit einer Tellerfedernsäule.
Eine kombinierte Federkennlinie (5), die bei bestimmten Einfederungszuständen die Krafteigenschaften abrupt verändert, kann mit kombinierten Federbauformen und speziellen Reihen– oder Mischschaltungen von Einzelfedern erreicht werden.
Die Federrate (R) ist die Steigung der Federkennlinie im Federdiagramm. Bei linearer Federkennlinie ist die Federrate konstant. Federn mit gekrümmter Federkennlinie besitzen eine veränderliche Federrate. Bei linearer Federkennlinie gilt:
Bei Druckfedern und Zugfedern
Bei Schenkelfedern / Drehfedern
Weitere Informationen:

Federsysteme sind federtechnische Anwendungen aus mehreren Einzelfedern, die gemeinsam spezielle Aufgaben verwirklichen. Diese individuell konstruierbaren Federsysteme können für die unterschiedlichsten Anwendungsarten konzipiert werden. Durch die Auswahl und die Anordnung verschiedener Federn lassen sich praktisch jede gewünschte Kräfteeigenschaft und jede Federkennlinie erzeugen. Ergänzend zu den klassischen Federsystemen – wie der Parallelschaltung und der Reihenschaltung – ist es möglich durch Mischschaltungen ganz besondere Federeigenschaften und Federkennlinien zu erzielen.
Die meisten Federsysteme sind Parallelschaltungen. Bei der Parallelschaltung kommt es darauf an, die einwirkende Kraft auf mehrere Federn zu verteilen. Ob die Federn dabei nebeneinander oder ineinander gestellt werden, hängt von dem zur Verfügung stehenden Bauraum ab. Nebeneinander stehende Federn sollten immer gleich sein. Die Federkonstante, bzw. Federrate der einzelnen Federn addieren sich und bilden eine neue Ersatzfeder, die höhere Kräfte bei kleinerem Federweg realisiert. So entsteht eine härtere Feder mit einer größeren Federkonstante und Federsteifigkeit. Auch werden mit einer Parallelschaltung die einzelnen Federn geringer belastet, wodurch sich die Lebensdauer und Dauerfestigkeit erhöhen. Formeln für die Berechnung des gesamten Federwegs, Federkraft und Federkonstante einer Parallelschaltung von Federn.
Die Reihenschaltung von Einzelfedern kommt seltener vor. Dabei werden die Federn mit Zwischenlagen hintereinander verbaut. Bei der Reihenschaltung wird, anders als bei der Parallelschaltung, die einwirkende Kraft auf jede Feder mit der gleichen Stärke abgegeben. Dadurch bildet sich eine Ersatzfeder, die eine kleinere Gesamtfederkonstante, bzw. Gesamtfederrate besitzt als die Federkonstanten der Einzelfedern und bei der sich die Federwege der einzelnen Federn addieren. Damit lässt sich nicht nur eine weiche Gesamtfeder mit einer geringen Federsteifigkeit und einem langsamen Kraftanstieg entwickeln, sondern mit der richtigen Federauswahl können in einer Reihenschaltung gezielt bestimmte Federkräfte in bestimmten Spannungszuständen erreicht werden. Somit lässt sich jede gewünschte Federkennlinie realisieren. Formeln für die Berechnung des gesamten Federwegs, Federkraft und Federkonstante einer Reihenschaltung von Federn.
Bei der Mischschaltung werden die Eigenschaften von Parallelschaltung und Reihenschaltung kombiniert. So lassen sich zum Beispiel Kräfte auf mehrere Federn mit einer progressiven Federkennlinie verteilen, indem übereinander angeordnete, unterschiedliche Parallelschaltungen eingesetzt werden. Neben dieser einfachen Mischschaltung können auch Federsysteme entwickelt werden, wo das Federsystem zuerst die Eigenschaften einer Reihenschaltung aufweist und im späteren Verlauf dann die Eigenschaften einer Parallelschaltung annimmt. Formel für die Berechnung der Gesamtfederkonstante einer Mischschaltung von Federn.
Die meisten Federsysteme werden mit Druckfedern realisiert. Es gibt aber auch klassische Federsysteme mit Zugfedern, wie zum Beispiel Garagentorfedersysteme oder auch Klappmechanismen für Bettkästen. Bei den Schenkelfedern wurde mit der Doppelschenkelfeder sogar eine klassische Parallelschaltung standardisiert umgesetzt.
Neben den Federsystemen aus Runddrahtfedern gibt es auch Federsysteme mit Wellen- und Tellerfedern. Der Vorteil bei dieser Art von Federn ist die größere Kraftaufnahme auf kleinem Raum, der Nachteil ist ein geringer Federweg; dieser kann nur durch eine größere Wellenfedersäule ausgeglichen werden, womit der Raumvorteil wieder verloren geht. Bei Federsystemen aus Runddraht ist zwar der Bauraum zur Umsetzung der Federanwendung unter Umständen größer, jedoch kann mit diesen Federsystemen jeder gewünschte Spannungszustand linear oder progressiv realisiert werden, und das bei deutlich geringeren Herstellungskosten.
Gutekunst Federn hat jahrzehntelange Erfahrung in der Auslegung von Federsystemen. Senden Sie bitte Ihre Anforderungen an technik@gutekunst-co.com, oder kontaktieren Sie direkt unsere Entwicklungsabteilung unter Telefon 035877 227-11.
Weitere Informationen:
Schenkelfedern, auch Drehfedern genannt, sind mechanische Kraftspeicher, die bei einer Winkel-/Drehbewegung an den Schenkeln ein Drehmoment aufnehmen, das sie beim Entspannen wieder abgeben. Schenkelfedern oder Drehfedern werden aus runden, ovalen oder vierkant Federstahldrähten hergestellt.  Der Federstahldraht wird dabei mehrheitlich im Kaltumformungsprozess, entweder durch Winden um einen Dorn oder bei vollautomatischen Federwindeautomaten mit Hilfe von Drahtführungsstiften in jede gewünschte Form gebracht. Die Fertigungstoleranzen werden von Gütegrad 1 (kleinste Toleranz) bis Gütegrad 3 (größte Toleranz) nach DIN 2194 festgelegt. Die Berechnung der Schenkelfedern oder Drehfedern erfolgt nach der Norm EN 13906-3. Zur Berechnung von Schenkelfedern oder Drehfedern stellt Gutekunst Federn das Federnberechnungsprogramm WinFSB zur freien Verfügung. Eine Formelsammlung zur Schenkelfedernberechnung kann hier heruntergeladen werden.
Der Federstahldraht wird dabei mehrheitlich im Kaltumformungsprozess, entweder durch Winden um einen Dorn oder bei vollautomatischen Federwindeautomaten mit Hilfe von Drahtführungsstiften in jede gewünschte Form gebracht. Die Fertigungstoleranzen werden von Gütegrad 1 (kleinste Toleranz) bis Gütegrad 3 (größte Toleranz) nach DIN 2194 festgelegt. Die Berechnung der Schenkelfedern oder Drehfedern erfolgt nach der Norm EN 13906-3. Zur Berechnung von Schenkelfedern oder Drehfedern stellt Gutekunst Federn das Federnberechnungsprogramm WinFSB zur freien Verfügung. Eine Formelsammlung zur Schenkelfedernberechnung kann hier heruntergeladen werden.
Schenkelfedern werden im Regelfall zylindrisch mit gleichbleibender Steigung ohne Windungsabstände hergestellt. Je nach Anwendungsfall können die Schenkel gerade tangential, radial innen oder außen, axial oder achsparallel usw. ausgeleitet werden. Nachfolgend eine Auswahl an möglichen Schenkelformen.
Standardmäßig gibt es die Schenkelfedern in den Schenkelstellungen 0/360 (A), 90 (B), 180(C) und 270° (D). Es kann jedoch über die Windungszahl jede benötigte Schenkelstellung erstellt werden.
Die Federleistung bei Schenkelfedern wird als Drehmoment in Nmm angegeben. Um die Federkraft in N zu berechnen, ist der Hebelarm (RH) (Entfernung vom Zentrum Federkörper bis zum Krafteinleitungspunkt am Schenkel) zu bestimmen und mit folgender Formel zu berechnen.
Die höchste erreichbare Federkraft (Fn) ergibt sich dann aus der Teilung von dem maximalen Drehmoment (Mn) durch den Hebelarm (RH):
Die erreichbare Kraft bei einem vorgegebenen Drehwinkel wird berechnet mit der Teilung der höchsten Federkraft (Fn) durch den maximalen Drehwinkel
multipliziert mit dem Drehwinkel:
Bei der Berechnung der Federkraft muss auch die Schenkeldurchbiegung (ß) berücksichtigt werden. Diese Schenkeldurchbiegung wird größer, je länger der Schenkel und je weiter weg der Krafteinleitungspunkt (RH) vom Zentrum des Federkörpers ist.
Zudem sollten Schenkelfedern immer nur in Windungsrichtung belastet werden. Aus diesem Grund werden Schenkelfedern baugleich links- und rechtsgewunden angeboten. Schenkelfedern haben meistens einem zylindrischen Federkörper mit einer linearen Federkennlinie. Anwendungsbeispiele mit einer progressiven Federkennlinie oder konisch zulaufenden Federkörpern sind uns nicht bekannt.
Federsysteme mit Schenkelfedern können in einer Parallelschaltung realisiert werden. Und weil es hervorragend funktioniert, hat man mit der Doppelschenkelfeder sogar einen eigenen Federntyp kreiert, um die Vorteile der Parallelschaltung zu nutzen.
Die Schenkelfedern aus dem Gutekunst Federn Katalogprogramm werden nach dem Winden nicht angelassen, was den Vorteil hat, dass Schenkelabbiegungen und Schenkelkürzungen jederzeit einfach selbst vorgenommen werden können. Ein Anlassen der Schenkelfedern ist grundsätzlich nicht notwendig, wenn die Biegespannung immer nur in Windungsrichtung erfolgt. Schenkelfedern dürfen also immer nur in Windungsrichtung belastet werden! Die Schenkelfedern arbeiten normalerweise über einen Dorn, der die Feder auf Position hält. Da der Federkörper sich aber bei der Drehbewegung verengt, muss bei der Wahl des inneren Windungsdurchmessers (Di) der kleinste und größte mögliche Dorndurchmesser berücksichtigt werden. Die durch die Führung entstehende Reibung beeinflusst das Federungsverhalten, welche sich in Form einer Hystereseschleife abbildet. Dabei wird ein Teil der Federarbeit in Wärme umgewandelt und geht somit verloren.
Zudem geht ein bestimmter Prozentsatz der Federkraft verloren, wenn die Feder über einen längeren Zeitraum bei höheren Temperaturen belastet wird. Diesen Kraftverlust nennt man Relaxation und er nimmt mit steigender Temperatur und Spannung zu. Übersteigt zudem, bei der Belastung der Schenkelfeder, die Biegespannung den zulässigen Wert der Dehnungsgrenze, tritt eine bleibende Verformung ein, die sich in der unbelasteten Schenkelposition äußert. Um die Schenkelfeder für eine längere Lebensdauer auszulegen, sollte bei der Berechnung der Spannungskorrekturfaktor „q“ und die zulässige Hubspannung „σqh“ berücksichtigt werden. Zudem unterstützen eine durch kugelstrahlen verfestigte Oberfläche und eine reduzierte Belastung von bis zu 70 bis 80 Prozent der zulässigen Biegespannung die Lebensdauer.
Das Drehmoment bzw. die Federsteifigkeit hängen vom Federstahldraht und der Drehmomentrate bzw. Drehmomentkonstante ab. Die Drehmomentrate definiert auch das Verhältnis des Federmoments zum Drehwinkel. Grundsätzlich lässt sich die Dimensionierung des Drehmoments durch folgende Maßnahmen beeinflussen:
Drahtdurchmesser (d) größer > Feder härter
Windungsdurchmesser (De) größer > Feder weicher
Anzahl der Windungen (nt) größer > Feder weicher
Die Auswahl des Federstahldrahts beeinflusst nicht nur die Federkraft, sondern bietet auch für die verschiedenen Federanwendungen die passenden Werkstoffeigenschaften. So werden neben den normalen unlegierten Federstahldrähten, ebenso rostfreie Federstähle, SiCr-legierte Ventilfederdrähte, Kupferlegierungen für gute elektrische Eigenschaften, Nickellegierungen für hohe Wärme- und Korrosionsbeständigkeit, sowie Titanlegierungen für höchste Ansprüche aus der Luftfahrtechnik verwendet. Zudem stehen auch verschiedene Oberflächenbehandlungen zur Verfügung, um die Anforderungen der Feder zu optimieren.
Schenkelfedern werden bei Gutekunst Federn Katalogprogramm in 1600 Standardbaugrößen ab Lager angeboten, oder individuell nach Kundenanforderungen hergestellt.
Weiterführende Links:
 Die richtige Metallfeder für den gewünschten Einsatzzweck auszuwählen ist nicht immer einfach. In vielen Fachbüchern mit konstruktiven Grundlagen wird das Thema Federn sehr allgemein abgehandelt.
Die richtige Metallfeder für den gewünschten Einsatzzweck auszuwählen ist nicht immer einfach. In vielen Fachbüchern mit konstruktiven Grundlagen wird das Thema Federn sehr allgemein abgehandelt.
Falls Sie auf der Suche nach einer Standardfeder sind, finden Sie in unserem Lagerprogramm ein umfangreiches Federnsortiment mit 12.600 Baugrößen in Normalstahl und Edelstahl. Wenn nicht, haben wir nachfolgend die wichtigsten Parameter zur Auswahl der passenden Metallfeder zusammengestellt.
Zu Beginn eine kurze Übersicht zu den unterschiedlichen Federnarten:
Druckfedern
Druckfedern werden mit Abstand am häufigsten eingesetzt. Das liegt nicht nur an der Richtung der Krafteinwirkung, sondern vor allem an den besseren Belastungseigenschaften der Druckfeder. Denn Druckfedern können besser mit größeren Kräften und für Dauerfestigkeitsanwendungen mit Lastwechseln über 107 umgehen. Neben der großen Auswahl an Material für die unterschiedlichen Anwendungen kann bei der Druckfeder die Einsatzvielfalt mit verschiedensten Oberflächenbehandlungen problemlos erweitert werden. Aufgrund der Leistungsdaten der Druckfeder ist es in manchen Fällen sogar sinnvoller, eine Zugfederanwendung auf eine Druckfeder umzubauen.
Zugfedern
Zugfedern werden am zweithäufigsten eingesetzt. Überall dort, wo die Krafteinwirkung nicht auf Druck, sondern auf Zug erbracht werden muss, kommt man an der Zugfeder nicht vorbei. Insbesondere die spezielle Bauform mit den beidseitigen Ösen birgt einige Risiken, die bei der Zugfederauslegung berücksichtigt werden müssen. Auch, dass die Zugfeder bei einem Federbruch ihre Federkraft komplett verliert, sollte bei der Verwendung einer Zugfeder beachtet werden. Mit der Materialauswahl ist die Einsatzvielfalt der Zugfeder bereits größtenteils ausgeschöpft, da aufgrund der aneinander liegenden Windungen das Aufbringen einer Oberflächenbehandlung nur mit einem erhöhten Aufwand möglich ist.
Schenkelfedern
Schenkelfedern werden bei Drehbewegungen eingesetzt, also überall dort, wo eine Biegebeanspruchung auftritt. Bei den Schenkelfedern gibt es keine besonderen Bauformen, d. h. der Federkörper einer Schenkelfeder ist immer zylindrisch mit einer linearen Federkennlinie. Bei den Schenkelfedern kommt es eher auf die individuelle Schenkelform an, die optimal zur Krafteinleitung der Drehbewegung angeformt wird. Wie bei der Zugfeder ist es auch bei der Schenkelfeder durch die aneinander liegenden Windungen schwierig, weitere Eigenschaften durch eine nachträgliche Oberflächenbehandlung aufzubringen.
Grundsätzlich werden Metallfedern nach ihrer Kennlinie beurteilt. Die Federkennlinie ist der Charakter der Metallfedern. Diese stellt das Verhältnis der Federkraft „F“ zum Federweg „s“ dar. Je nach Federntyp, Federnbauform, Windungsabstand und Federsystem kann man lineare, progressive, degressive oder kombinierte Federkennlinien erzeugen. Bei einer linearen Federkennlinie (Bild b: zylindrische Feder) wird die Kraft gleichmäßig abgegeben, bei einer progressiven Kennlinie (Bild a: konische Feder) verstärkt sich die Kraftentfaltung mit Zunahme der Belastung und bei einer degressiven Kennlinie (Bild c: Tellerfeder) verringert sich die Kraftentfaltung mit der Belastung.
Bei der kombinierten Federkennlinie (Bild d: Kennlinie 5) werden unterschiedliche Kräftezustände entlang der Federkennlinie abgebildet. Diese kombinierte Federkennlinie kann mithilfe von Federsystemen erzeugt werden.
Nachdem man sich mit der Federkennlinie bzw. dem Kraftverlauf auf den Charakter der Metallfeder festgelegt hat, müssen zur optimalen Auslegung der Metallfeder folgende Anforderungen abgeklärt und festgelegt werden:
Die Einsatztemperatur beeinflusst entscheidend die Auswahl des passenden Werkstoffs. Aus diesem Grund gibt es bevorzugte Federstähle für Niedrigtemperatur- und für Hochtemperaturanwendungen. Besonders bei Hochtemperaturanwendungen muss die Relaxation des Federwerkstoffs bei der Kräfteauslegung berücksichtigt werden. Dabei tritt unter permanenter Spannung und höheren Temperaturen ein Kraftverlust auf, der mit steigender Temperatur und Belastungsdauer zunimmt.
In welcher Umgebung wird die Metallfeder eingesetzt? Muss die Feder korrosionsbeständig sein oder gegen aggressive Säuren bestehen? Wird sie in der Lebensmittelbranche eingesetzt oder muss sie medizinisch rein sein? Alle diese Fragen beeinflussen die Auswahl des Federstahldrahts und einer möglichen abschließenden Oberflächenbehandlung.


Welche Federkräfte soll die Metallfeder bei bestimmten Federwegen erzeugen? Meistens werden die Federn vorgespannt eingebaut, d. h. die Feder erzeugt bereits eine bestimmte Vorspannkraft im Ruhezustand. Diese Kraft wird als „F1“ vorgespannte Federkraft beschrieben. Dazu muss die benötigte Federkraft benannt werden, welche die Feder im gespannten Zustand erreichen soll. Diese Federkraft wird als „F2“ gespannte Federkraft beschrieben. Zu diesen beiden Federkräften müssen noch die jeweiligen Federwege „s1“ und „s2“ oder Federlängen „L1“ und „L2“ bestimmt werden. Besonders bei dynamischen Belastungen kommt es auf den Federhub „sh“ an, der den Federweg zwischen „s1“ und „s2“, bzw. zwischen „L1“ und „L2“ beschreibt. Je kleiner der Federhub ist, umso besser ist die dynamische Belastbarkeit der Metallfeder.
Welche Dimensionen hat der Einbauraum, in der die Feder eingesetzt werden soll? Welchen Durchmesser und welche Länge darf bzw. muss die Metallfeder besitzen, damit sie eingebaut werden kann? Diese Baumaße sind Voraussetzung für die Auslegung der passenden Federn. Dabei müssen auch die Toleranzwerte der jeweiligen Maße im ruhenden und belasteten Zustand berücksichtigt werden.
Dazu muss, je nach Druck-, Zug- oder Schenkelfeder, die Einbausituation überprüft werden. Wird z. B. die Druckfeder durch einen Dorn oder innerhalb einer Hülse geführt, muss die Reibung während der Federarbeit in einer Hystereseschleife berücksichtigt werden. Wird die Druckfeder ohne Führung eingebaut, müssen die unterschiedlichen Knickgrenzen für die verschiedenen Federendlagerungen berücksichtigt werden. Bei Zugfedern ist dagegen wichtig, an welcher Position die Ösen eingehängt werden. So ist die optimale Krafteinwirkung bei Zugfedern zentrisch an beiden Ösen entlang der Federlängsachse. Sehr häufig werden Ösen auch seitlich ausgelegt. Das muss entsprechend bei der Federauslegung berücksichtigt werden. Und bei der Schenkelfeder müssen die Schenkelform und die Windungsrichtung der Einbausituation angepasst werden. Zudem ist es bei Schenkelfedern wichtig, dass diese immer nur in Windungsrichtung belastet werden.
Abschließend ist das Toleranzfeld der jeweiligen Federnart zu berücksichtigen. Denn jede Metallfeder wird bei der Produktion innerhalb eines bestimmten Toleranzfeldes gefertigt, sodass die Feder optimal für den Einsatzfall hergestellt wird. Dieses Toleranzfeld wird bei Metallfedern in Gütegrad 1, 2 und 3 ausgewiesen. Normalerweise werden Metallfedern in Gütegrad 2 gefertigt, was vor allem bei kleineren Federabmessungen einem Toleranzfeld von bis zu zehn Prozent entspricht. Bei Gütegrad 1, mit höheren Herstellungskosten, ist das Toleranzfeld am kleinsten und bei Gütegrad 3, mit geringeren Herstellungskosten, am größten.
Zusammenfassend noch einmal alle wichtigen Federparameter für eine optimale Federnauswahl und Federnauslegung der Metallfeder:
Federnart
► Druckfeder · Zugfeder · Schenkelfeder · Tellerfeder · Federsystem
Federkennlinie
► linear · progressiv · degressiv · kombiniert
Belastungsart und Lebensdauer
► statisch · dynamisch
Lebensdauer
► Lastwechsel (Federhübe) gesamt
Einsatztemperatur
► Umgebungstemperatur in der die Feder eingesetzt wird
Umgebungsmedium
► Flüssigkeiten, Gase … in der die Feder eingesetzt wird
Federkräfte bei bestimmten Federwegen bzw. Federlängen
► vorgespannte Federkraft = F1 bei s1 oder L1
► gespannte Federkraft = F2 bei s2 oder L2
F1 vorgespannte Federkraft in N
s1 Federweg vorgespannt oder L1 Federlänge vorgespannt
F2 gespannte Federkraft in N
s2 Federweg gespannt oder L2 Federlänge gespannt
Vorhandener Einbauraum
► Länge und Breite des Einbauraums
► Länge Feder zwischen Krafteinleitungspunkten
Einbausituation
bei Druckfedern
► Führung durch Dorn und/oder Hülse
► ohne Führung die Knickgrenze der Federendlagerung beachten
bei Zugfedern
► Krafteinwirkung zentral oder dezentral
► Ösenstellung (Verdrehwinkel der Ösen zueinander) und Ösenposition (zentrisch/seitlich)
bei Schenkelfedern
► Schenkelform zur optimalen Kraftaufnahme
► Windungsrichtung der Belastung
Metallfedern mit einer linearen Federkennlinie, in den Federwerkstoffen Normalstahl EN 10270-1 und rostfrei EN 10270-3-1.4310, findet man in 12.600 Federbaugrössen im Gutekunst Federnkatalog. Bei allen nicht linearen Federanwendungen senden Sie bitte die benötigten Federparameter einfach an verkauf@gutekunst-co.com oder nutzen Sie das Gutekunst Anfrageformular.
Weiterführende Links:
Beschreibung Formelzeichen Zugfedern
Vor der Auslegung der Zugfeder muss geklärt werden, ob es sich bei der vorgesehenen Beanspruchungsart um eine statische oder um eine dynamische Beanspruchung handelt.
Zeitlich konstante (ruhende) Belastung, bzw. zeitlich veränderliche Belastung mit weniger als 10 000 Hüben insgesamt oder kleinen Hubspannungen (τh = τ2 – τ1) bis 0,1 x Dauerhubfestigkeit (τkh = τk2 – τk1).
Als dynamische Beanspruchung bei Federn gilt, zeitlich veränderliche Beanspruchungen mit mehr als 10 000 Lastwechseln oder Hubspannungen (τh) über 0,1 x Dauerhubfestigkeit (τkh) bei konstanter und veränderlicher Hubspannung.
Die vorhandene Schubspannung wird wie folgt ermittelt.
Schubspannung aus Kraft:
Schubspannung aus Weg:
Für die dynamische Beanspruchung muss wegen der Spannungserhöhung die korrigierte Hubspannung berechnet werden.
Korrigierte Schubspannung:
Korrigierte Hubspannung: τkh = τk2 – τk1
Wobei für k gilt (nach Bergsträsser):
Mit dem Spannungskorrekturfaktor k, der vom Wickelverhältnis (Verhältnis von mittlerem Durchmesser zur Drahtstärke) der Feder abhängt, kann die höchste Spannung annähernd ermittelt werden.
Zulässige Spannung:
Mindestzugfestigkeitswerte Federwerkstoffe
Die vorhandene maximale Spannung τn beim größten Federweg sn wird der zulässigen Spannung gleichgesetzt. Um jedoch Relaxation zu vermeiden, sollte in der Praxis nur 80 % dieses Federweges ausgenutzt werden.
Für dynamische Beanspruchungen können keine allgemeingültigen Dauerfestigkeitswerte angegeben werden, da an den Biegestellen der Ösen zusätzliche Spannungen auftreten können, die zum Teil über die zulässigen Spannungen hinausgehen können. Zugfedern sollten daher möglichst nur statisch beansprucht werden. Wenn sich dynamische Beanspruchung nicht vermeiden lässt, sollte man auf angebogene Ösen verzichten und eingerollte bzw. eingeschraubte Endstücke einsetzen. Sinnvoll ist ein Lebensdauertest unter späteren Einsatzbedingungen. Eine Oberflächenverfestigung durch Kugelstrahlen ist wegen der eng aneinander liegenden Windungen nicht oder nur mit großem Aufwand durchführbar.
Interessante Links:

Ein Sprengring ist eine besondere Form des Sicherungsrings. Im Maschinenbau sichert er formschlüssig Bauteile wie Räder, Dichtelemente und Lager auf Achsen, Wellen oder innerhalb von Bohrungen gegen eine axiale Verschiebung.
Warum heißt er so? Die Bezeichnung Sprengring leitet sich von der früheren Herstellungsmethode ab: Damals wurde er von Rohren abgeschnitten und anschließend aufgetrennt. Heute bestehen Sprengringe aus Federstahldraht mit gleichbleibendem Querschnitt. An einem Windeautomaten werden sie zu einem Ring gebogen. Der Durchmesser kann wenige Millimeter bis zu einigen Metern betragen.
Sprengringe nehmen die Kräfte auf, die in Richtung einer Achse des Rotationskörpers wirken. Das Sicherungselement fixiert das jeweilige Bauteil und verhindert, dass es sich axial in den Lagersitzen verschiebt. Sprengringe sind vielseitig anwendbar und bieten in vielen unterschiedlichen Fällen die beste und kostengünstigste Lösung.
Sprengringe sind in zwei grundsätzlichen Ausführungen erhältlich: Für den Wellenbau und für Bohrungen. Für jede Anwendung ist eine spezielle DIN-Variante vorhanden.
Um einen Sprengring auf eine Welle zu setzen, wird sie an einer entsprechenden Stelle eingekerbt und eine Nut eingefügt. Diese ist etwa 0,1 bis 0,2 mm breiter als der Ring selbst. Um eine Deformation des Wellensicherungsrings zu vermeiden, kann zusätzlich ein konischer Montagedorn auf das Wellenende gesetzt oder eine dünnwandige Hülse über die Welle gestreift werden. Mittels einer Sprengzange wird der aufgeweitete Ring über die Welle geschoben.
Bei Bedarf findet man im Gutekunst Federnkatalog die Sprengringe für Wellendurchmesser von 4 bis 125 mm in den Federwerkstoffen Normalstahl EN 10270-1 und Edelstahl EN 10270-3-1.4310 ab Lager. Hier geht es zur Artikelauswahl Sprengringe für Wellen
Bei einer Bohrung erfolgt der Einbau des Sprengrings ähnlich wie bei einer Welle, lediglich die Einkerbung ist meist tiefer. Konische Hülsen vereinfachen die Montage der Bohrungssicherungsringe. Die Ringe werden ebenfalls mit einer Sprengzange in die Bohrung eingesetzt. Beim Einbau in Getriebe lassen sich die Sprengringe zusätzlich als Abstandshalter einsetzen.
Bei Bedarf findet man im Gutekunst Federnkatalog die Sprengringe für Bohrungsdurchmesser von 7 bis 125 mm in den Federwerkstoffen Normalstahl EN 10270-1 und Edelstahl EN 10270-3-1.4310 ab Lager. Hier geht es zur Artikelauswahl Sprengringe für Bohrungen

Sprengringe, die aus Runddraht gefertigt sind, lassen sich auch als Federringe zur Schraubensicherung einsetzen. Da die Enden des Federrings nicht zueinander fluchten, erzeugen sie bei der radialen Anziehbewegung eine axiale Kraft. Kommt es zu Erschütterungen, ist die Verschraubung fest geschützt und kann sich nicht selbständig lösen. Auf diese Weise werden zum Beipsiel Eisenbahnschienen gesichert.
Gutekunst bietet Ihnen in seinem Katalog ein Standardprogramm an Sprengringen für Wellen- und Bohrungssicherungen. Darüber hinaus entwickeln und produzieren wir auch Sprengringe nach Ihren individuellen Vorgaben, die sich optimal Ihren Bedürfnissen anpassen. Senden Sie dafür bitte Ihre Anforderungen einfach an Fax (+49) 07123 960-150 oder technik@gutekunst-co.com
Der Elastizitätsmodul ist ein Materialkennwert aus der Werkstofftechnik. Dieser Kennwert beschreibt den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers in einem linear-elastischem Verhalten. Der Elastizitätsmodul ist unter den Abkürzungen E-Modul oder als Formelzeichen E in der Federnberechnung bekannt; er hat die Einheit „N/mm²“ einer mechanischen Spannung.
Je mehr Widerstand ein Material seiner elastischen Verformung entgegensetzt, umso größer ist der Betrag des Elastizitätsmoduls. Ein Bauteil aus einem Material mit hohem Elastizitätsmodul (beispielsweise Federstahl) ist somit steifer als ein Bauteil gleicher Konstruktion (mit identischen geometrischen Abmessungen), das aus einem Material mit niedrigem Elastizitätsmodul (beispielsweise Gummi) besteht. Dabei ist der Elastizitätsmodul die Proportionalitätskonstante im Hookeschen Gesetz.
Rm = Zugfestigkeit
σ = Spannung
AL = Lüdersdehnung
Ag = Gleichmaßdehnung
A = Bruchdehnung
At = gesamte Dehnung bei Bruch
Ɛ = Dehnung
Die Definition des Elastizitätsmoduls: Der Elastizitätsmodul ist die Steigung des Graphen im Spannungs-Dehnungs-Diagramm bei einachsiger Belastung innerhalb des linearen Elastizitätsbereichs. Dieser lineare Bereich heißt auch Hookesche Gerade.
Dabei bezeichnet
σ = F/A (=Kraft/Fläche) die mechanische Spannung (Normalspannung, nicht Schubspannung) und Ɛ = ∆L/L0 die Dehnung. Die Dehnung ist das Verhältnis von Längenänderung ∆L = L – L0 zur ursprünglichen Länge L0
E – Elastizitätsmodul
σ – Spannung
ε – Dehnung
Hier gibt es das Elastizitätsmodul zur Federnberechnung bei Raumtemperatur (20°C) für die wichtigsten Federwerkstoffe.
Der Elastizitätsmodul ist aber nicht bezüglich aller physikalischen Größen konstant. So beeinflussen zudem die unterschiedlichen Umgebungseinflüsse, wie zum Beispiel Temperatur oder Feuchte, den E-Modul. Die Anpassung des Elastizitätsmoduls wird bei höheren Temperaturen nach folgender Formel ermittelt, wobei die Federwerkstoffkennwerte bei Raumtemperatur (20°C) als Basis dienen.
Weitere Informationen:
Die Norm DIN 2098 beinhaltet eine Auswahl an kaltgeformten zylindrischen Druckfedern ab 0,1 bis 10 mm Drahtstärke in 525 standardisierten Druckfederabmessungen. Die Druckfedern sind in Gütegrad 2 nach DIN EN 15800 aus normalen Federstahldraht EN 10207-1DH (bis 1,8 mm Drahtstärke) und -1SH (ab 1,8 mm Drahtstärke) gefertigt. Sie sind rechtsgewickelt (im Uhrzeigersinn) mit gleichmäßiger Steigung. Bis Drahtdurchmesser 0,45 mm sind die Endwindungen „angelegt“, größere Drahtstärken haben „angelegte und geschliffene“ Endwingungen. Die Druckfedern sind angelassen und werden je nach Setzverhalten, vorgesetzt.
Heute hat die Norm DIN 2098, die früher für eine schnelle Druckfedernauswahl und Belieferung in kleinen Stückzahlen sorgen sollte, seine Wertigkeit verloren. Viele Federnhersteller haben längst ihr Artikelangebot auf Basis der Norm DIN 2098 erweitert. So auch Gutekunst Federn, die heute in ihrem Federnkatalog ein Standardsortiment mit 12.603 Abmessungen ab Lager anbietet. Nachfolgend zusammengefasst die Druckfederabmessungen nach DIN 2098 Blatt 1 und 2.
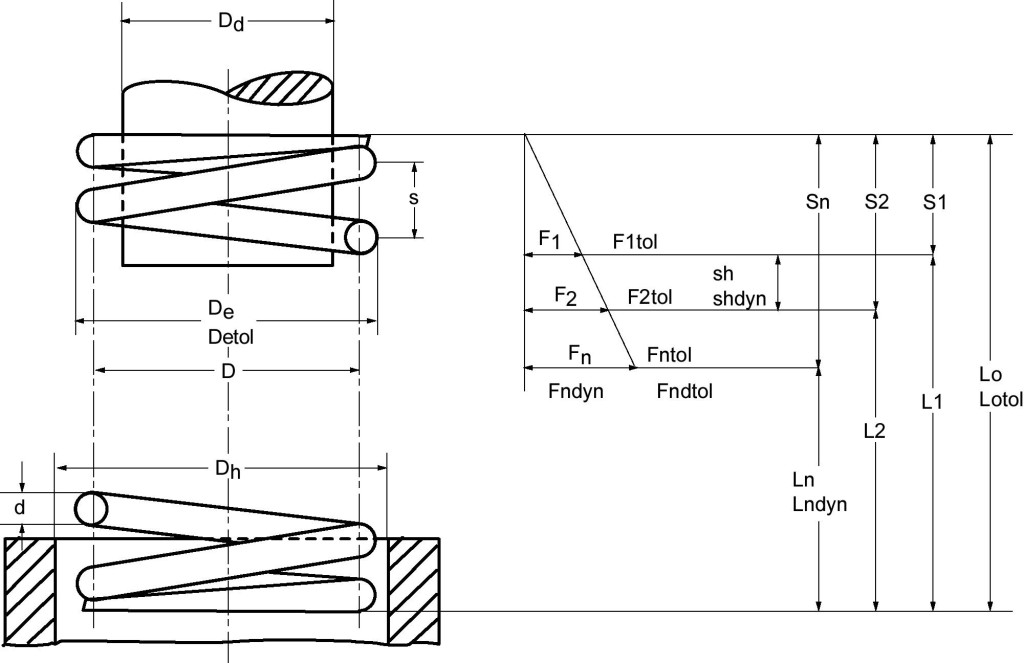
d Drahtdurchmesser (mm)
D Mittlerer Windungsdurchmesser (mm)
Dd Größter Dorndurchmesser (mm)
Fn Höchstkraft bei statischer Belastung (N)
L0 Ungespannte Länge der Feder (mm)
sn Größter Federweg bei statischer Belastung (mm)
n Anzahl der federnden Windungen (St.)
R Federrate (N/mm)
Gew Gewicht pro Stück (g)
| Artikelnummer | d (mm) | D (mm) | Dd (mm) | Dh (mm) | Fn (N) | L0 (mm) | sn (mm) | n (St) | R (N/mm) | Gew (g) |
|---|---|---|---|---|---|---|---|---|---|---|
| D-2020 | 0.1 | 0.5 | 0.3 | 0.8 | 0.582 | 1 | 0.25 | 3.5 | 2.329 | 0.0005 |
| D-2021 | 0.1 | 0.5 | 0.3 | 0.8 | 0.629 | 1.4 | 0.42 | 5.5 | 1.482 | 0.0007 |
| D-2022 | 0.1 | 0.5 | 0.3 | 0.8 | 0.655 | 2 | 0.68 | 8.5 | 0.959 | 0.001 |
| D-2023 | 0.1 | 0.5 | 0.3 | 0.8 | 0.605 | 2.7 | 0.93 | 12.5 | 0.652 | 0.0014 |
| D-2024 | 0.1 | 0.5 | 0.3 | 0.8 | 0.637 | 3.9 | 1.45 | 18.5 | 0.441 | 0.002 |
| D-2015 | 0.1 | 0.63 | 0.4 | 0.9 | 0.517 | 1.2 | 0.44 | 3.5 | 1.164 | 0.0007 |
| D-2016 | 0.1 | 0.63 | 0.4 | 0.9 | 0.528 | 1.7 | 0.71 | 5.5 | 0.741 | 0.0009 |
| D-2017 | 0.1 | 0.63 | 0.4 | 0.9 | 0.51 | 2.4 | 1.06 | 8.5 | 0.479 | 0.0013 |
| D-2018 | 0.1 | 0.63 | 0.4 | 0.9 | 0.522 | 3.4 | 1.6 | 12.5 | 0.326 | 0.0018 |
| D-2019 | 0.1 | 0.63 | 0.4 | 0.9 | 0.53 | 4.9 | 2.4 | 18.5 | 0.22 | 0.0025 |
| D-2010 | 0.1 | 0.8 | 0.5 | 1.1 | 0.416 | 1.5 | 0.73 | 3.5 | 0.568 | 0.0009 |
| D-2011 | 0.1 | 0.8 | 0.5 | 1.1 | 0.431 | 2.2 | 1.19 | 5.5 | 0.362 | 0.0012 |
| D-2012 | 0.1 | 0.8 | 0.5 | 1.1 | 0.429 | 3.2 | 1.83 | 8.5 | 0.234 | 0.0016 |
| D-2013 | 0.1 | 0.8 | 0.5 | 1.1 | 0.439 | 4.6 | 2.76 | 12.5 | 0.159 | 0.0023 |
| D-2014 | 0.1 | 0.8 | 0.5 | 1.1 | 0.434 | 6.6 | 4.04 | 18.5 | 0.108 | 0.0032 |
| D-2005 | 0.1 | 1 | 0.7 | 1.4 | 0.353 | 2 | 1.21 | 3.5 | 0.291 | 0.0011 |
| D-2006 | 0.1 | 1 | 0.7 | 1.4 | 0.345 | 2.9 | 1.86 | 5.5 | 0.185 | 0.0015 |
| D-2007 | 0.1 | 1 | 0.7 | 1.4 | 0.358 | 4.4 | 2.99 | 8.5 | 0.12 | 0.002 |
| D-2008 | 0.1 | 1 | 0.7 | 1.4 | 0.358 | 6.3 | 4.39 | 12.5 | 0.082 | 0.0028 |
| D-2009 | 0.1 | 1 | 0.7 | 1.4 | 0.36 | 9.2 | 6.54 | 18.5 | 0.055 | 0.004 |
| D-2000 | 0.1 | 1.2 | 0.8 | 1.5 | 0.301 | 2.6 | 1.79 | 3.5 | 0.168 | 0.0013 |
| D-2001 | 0.1 | 1.2 | 0.8 | 1.5 | 0.292 | 3.8 | 2.73 | 5.5 | 0.107 | 0.0018 |
| D-2002 | 0.1 | 1.2 | 0.8 | 1.5 | 0.3 | 5.8 | 4.33 | 8.5 | 0.069 | 0.0025 |
| D-2003 | 0.1 | 1.2 | 0.8 | 1.5 | 0.302 | 8.4 | 6.41 | 12.5 | 0.047 | 0.0034 |
| D-2004 | 0.1 | 1.2 | 0.8 | 1.5 | 0.306 | 12.4 | 9.62 | 18.5 | 0.032 | 0.0048 |
| D-2046 | 0.12 | 0.63 | 0.4 | 0.9 | 1.479 | 1.2 | 0.44 | 2.5 | 3.379 | 0.0008 |
| D-2047 | 0.12 | 0.63 | 0.4 | 0.9 | 0.809 | 1.7 | 0.53 | 5.5 | 1.536 | 0.0013 |
| D-2048 | 0.12 | 0.63 | 0.4 | 0.9 | 0.811 | 2.4 | 0.82 | 8.5 | 0.994 | 0.0019 |
| D-2049 | 0.12 | 0.63 | 0.4 | 0.9 | 0.857 | 3.4 | 1.27 | 12.5 | 0.676 | 0.0026 |
| D-2050 | 0.12 | 0.63 | 0.4 | 0.9 | 0.889 | 4.9 | 1.95 | 18.5 | 0.457 | 0.0036 |
| D-2041 | 0.12 | 0.8 | 0.5 | 1.2 | 0.696 | 1.5 | 0.59 | 3.5 | 1.179 | 0.0012 |
| D-2042 | 0.12 | 0.8 | 0.5 | 1.2 | 0.683 | 2.1 | 0.91 | 5.5 | 0.75 | 0.0017 |
| D-2043 | 0.12 | 0.8 | 0.5 | 1.2 | 0.723 | 3.1 | 1.49 | 8.5 | 0.485 | 0.0024 |
| D-2044 | 0.12 | 0.8 | 0.5 | 1.2 | 0.736 | 4.4 | 2.23 | 12.5 | 0.33 | 0.0033 |
| D-2045 | 0.12 | 0.8 | 0.5 | 1.2 | 0.734 | 6.3 | 3.29 | 18.5 | 0.223 | 0.0046 |
| D-2036 | 0.12 | 1 | 0.6 | 1.4 | 0.588 | 1.9 | 0.97 | 3.5 | 0.604 | 0.0015 |
| D-2037 | 0.12 | 1 | 0.6 | 1.4 | 0.57 | 2.7 | 1.49 | 5.5 | 0.384 | 0.0021 |
| D-2038 | 0.12 | 1 | 0.6 | 1.4 | 0.584 | 4 | 2.35 | 8.5 | 0.249 | 0.0029 |
| D-2039 | 0.12 | 1 | 0.6 | 1.4 | 0.604 | 5.8 | 3.57 | 12.5 | 0.169 | 0.0041 |
| D-2040 | 0.12 | 1 | 0.6 | 1.4 | 0.606 | 8.4 | 5.31 | 18.5 | 0.114 | 0.0058 |
| D-2030 | 0.12 | 1.2 | 0.8 | 1.6 | 0.508 | 2.4 | 1.46 | 3.5 | 0.349 | 0.0019 |
| D-2031 | 0.12 | 1.2 | 0.8 | 1.6 | 0.501 | 3.5 | 2.26 | 5.5 | 0.222 | 0.0025 |
| D-2032 | 0.12 | 1.2 | 0.8 | 1.6 | 0.504 | 5.2 | 3.51 | 8.5 | 0.144 | 0.0035 |
| D-2033 | 0.12 | 1.2 | 0.8 | 1.6 | 0.509 | 7.5 | 5.21 | 12.5 | 0.098 | 0.0049 |
| D-2034 | 0.12 | 1.2 | 0.8 | 1.6 | 0.509 | 10.9 | 7.71 | 18.5 | 0.066 | 0.0069 |
| D-2025 | 0.12 | 1.6 | 1.2 | 2.1 | 0.384 | 3.6 | 2.61 | 3.5 | 0.147 | 0.0025 |
| D-2026 | 0.12 | 1.6 | 1.2 | 2.1 | 0.382 | 5.4 | 4.08 | 5.5 | 0.094 | 0.0034 |
| D-2027 | 0.12 | 1.6 | 1.2 | 2.1 | 0.387 | 8.2 | 6.39 | 8.5 | 0.061 | 0.0047 |
| D-2028 | 0.12 | 1.6 | 1.2 | 2.1 | 0.385 | 11.8 | 9.33 | 12.5 | 0.041 | 0.0065 |
| D-2029 | 0.12 | 1.6 | 1.2 | 2.1 | 0.389 | 17.4 | 13.95 | 18.5 | 0.028 | 0.0092 |
| D-2071 | 0.16 | 0.8 | 0.4 | 1.2 | 1.501 | 1.6 | 0.4 | 3.5 | 3.726 | 0.0022 |
| D-2072 | 0.16 | 0.8 | 0.4 | 1.2 | 1.515 | 2.2 | 0.64 | 5.5 | 2.371 | 0.003 |
| D-2073 | 0.16 | 0.8 | 0.4 | 1.2 | 1.523 | 3.1 | 0.99 | 8.5 | 1.534 | 0.0042 |
| D-2074 | 0.16 | 0.8 | 0.4 | 1.2 | 1.633 | 4.4 | 1.57 | 12.5 | 1.043 | 0.0058 |
| D-2075 | 0.16 | 0.8 | 0.4 | 1.2 | 1.602 | 6.2 | 2.27 | 18.5 | 0.705 | 0.0082 |
| D-2066 | 0.16 | 1 | 0.6 | 1.3 | 1.318 | 1.9 | 0.69 | 3.5 | 1.908 | 0.0027 |
| D-2067 | 0.16 | 1 | 0.6 | 1.3 | 1.36 | 2.7 | 1.12 | 5.5 | 1.214 | 0.0037 |
| D-2068 | 0.16 | 1 | 0.6 | 1.3 | 1.307 | 3.8 | 1.66 | 8.5 | 0.785 | 0.0052 |
| D-2069 | 0.16 | 1 | 0.6 | 1.3 | 1.347 | 5.4 | 2.52 | 12.5 | 0.534 | 0.0072 |
| D-2070 | 0.16 | 1 | 0.6 | 1.3 | 1.375 | 7.8 | 3.81 | 18.5 | 0.361 | 0.0102 |
| D-2061 | 0.16 | 1.2 | 0.8 | 1.6 | 1.078 | 2.2 | 0.98 | 3.5 | 1.104 | 0.0033 |
| D-2062 | 0.16 | 1.2 | 0.8 | 1.6 | 1.122 | 3.2 | 1.6 | 5.5 | 0.702 | 0.0045 |
| D-2063 | 0.16 | 1.2 | 0.8 | 1.6 | 1.15 | 4.7 | 2.53 | 8.5 | 0.455 | 0.0063 |
| D-2064 | 0.16 | 1.2 | 0.8 | 1.6 | 1.166 | 6.7 | 3.77 | 12.5 | 0.309 | 0.0087 |
| D-2065 | 0.16 | 1.2 | 0.8 | 1.6 | 1.177 | 9.7 | 5.63 | 18.5 | 0.209 | 0.0123 |
| D-2056 | 0.16 | 1.6 | 1.1 | 2.1 | 0.857 | 3.1 | 1.84 | 3.5 | 0.466 | 0.0044 |
| D-2057 | 0.16 | 1.6 | 1.1 | 2.1 | 0.901 | 4.7 | 3.04 | 5.5 | 0.296 | 0.006 |
| D-2058 | 0.16 | 1.6 | 1.1 | 2.1 | 0.909 | 7 | 4.74 | 8.5 | 0.192 | 0.0084 |
| D-2059 | 0.16 | 1.6 | 1.1 | 2.1 | 0.905 | 10 | 6.94 | 12.5 | 0.13 | 0.0116 |
| D-2060 | 0.16 | 1.6 | 1.1 | 2.1 | 0.911 | 14.6 | 10.34 | 18.5 | 0.088 | 0.0164 |
| D-2051 | 0.16 | 2 | 1.5 | 2.5 | 0.714 | 4.3 | 2.99 | 3.5 | 0.238 | 0.0055 |
| D-2052 | 0.16 | 2 | 1.5 | 2.5 | 0.723 | 6.5 | 4.77 | 5.5 | 0.152 | 0.0075 |
| D-2053 | 0.16 | 2 | 1.5 | 2.5 | 0.729 | 9.8 | 7.43 | 8.5 | 0.098 | 0.0105 |
| D-2054 | 0.16 | 2 | 1.5 | 2.5 | 0.732 | 14.2 | 10.97 | 12.5 | 0.067 | 0.0145 |
| D-2055 | 0.16 | 2 | 1.5 | 2.5 | 0.739 | 20.9 | 16.39 | 18.5 | 0.045 | 0.0205 |
| D-011R | 0.2 | 1 | 0.6 | 1.4 | 2.346 | 2 | 0.5 | 3.5 | 4.657 | 0.0043 |
| D-011S | 0.2 | 1 | 0.6 | 1.4 | 2.219 | 2.7 | 0.75 | 5.5 | 2.964 | 0.0059 |
| D-011T | 0.2 | 1 | 0.6 | 1.4 | 2.428 | 3.9 | 1.27 | 8.5 | 1.918 | 0.0082 |
| D-011U | 0.2 | 1 | 0.6 | 1.4 | 2.551 | 5.5 | 1.96 | 12.5 | 1.304 | 0.0113 |
| D-011V | 0.2 | 1 | 0.6 | 1.4 | 2.547 | 7.8 | 2.89 | 18.5 | 0.881 | 0.016 |
| D-011M | 0.2 | 1.2 | 0.8 | 1.7 | 2.135 | 2.3 | 0.79 | 3.5 | 2.695 | 0.0051 |
| D-011N | 0.2 | 1.2 | 0.8 | 1.7 | 2.111 | 3.2 | 1.23 | 5.5 | 1.715 | 0.007 |
| D-011O | 0.2 | 1.2 | 0.8 | 1.7 | 2.151 | 4.6 | 1.94 | 8.5 | 1.11 | 0.0098 |
| D-011P | 0.2 | 1.2 | 0.8 | 1.7 | 2.2 | 6.5 | 2.92 | 12.5 | 0.755 | 0.0136 |
| D-011Q | 0.2 | 1.2 | 0.8 | 1.7 | 2.208 | 9.3 | 4.33 | 18.5 | 0.51 | 0.0192 |
| D-011G | 0.2 | 1.6 | 1.1 | 2.1 | 1.777 | 3.1 | 1.56 | 3.5 | 1.137 | 0.0069 |
| D-011H | 0.2 | 1.6 | 1.1 | 2.1 | 1.725 | 4.4 | 2.38 | 5.5 | 0.724 | 0.0094 |
| D-011J | 0.2 | 1.6 | 1.1 | 2.1 | 1.717 | 6.4 | 3.67 | 8.5 | 0.468 | 0.0131 |
| D-011K | 0.2 | 1.6 | 1.1 | 2.1 | 1.754 | 9.2 | 5.51 | 12.5 | 0.318 | 0.0181 |
| D-011L | 0.2 | 1.6 | 1.1 | 2.1 | 1.758 | 13.3 | 8.17 | 18.5 | 0.215 | 0.0256 |
| D-007A | 0.2 | 2 | 1.5 | 2.6 | 0.713 | 4 | 1.93 | 5.5 | 0.37 | 0.0117 |
| D-008A | 0.2 | 2 | 1.5 | 2.6 | 1.417 | 5.9 | 3.83 | 5.5 | 0.37 | 0.0117 |
| D-009A | 0.2 | 2 | 1.5 | 2.6 | 1.408 | 8.7 | 5.88 | 8.5 | 0.24 | 0.0164 |
| D-010A | 0.2 | 2 | 1.5 | 2.6 | 1.43 | 12.6 | 8.78 | 12.5 | 0.163 | 0.0226 |
| D-011A | 0.2 | 2 | 1.5 | 2.6 | 1.429 | 18.3 | 12.98 | 18.5 | 0.11 | 0.032 |
| D-002 | 0.2 | 2.5 | 2 | 3.1 | 1.122 | 5.4 | 3.77 | 3.5 | 0.298 | 0.0107 |
| D-003 | 0.2 | 2.5 | 2 | 3.1 | 1.144 | 8.2 | 6.03 | 5.5 | 0.19 | 0.0146 |
| D-004 | 0.2 | 2.5 | 2 | 3.1 | 1.194 | 12.7 | 9.73 | 8.5 | 0.123 | 0.0205 |
| D-005 | 0.2 | 2.5 | 2 | 3.1 | 1.232 | 18.8 | 14.76 | 12.5 | 0.083 | 0.0283 |
| D-006 | 0.2 | 2.5 | 2 | 3.1 | 1.109 | 25.3 | 19.66 | 18.5 | 0.056 | 0.04 |
| D-026M | 0.25 | 1.2 | 0.7 | 1.8 | 3.502 | 2.4 | 0.53 | 3.5 | 6.58 | 0.008 |
| D-026N | 0.25 | 1.2 | 0.7 | 1.8 | 3.622 | 3.3 | 0.86 | 5.5 | 4.187 | 0.011 |
| D-026O | 0.25 | 1.2 | 0.7 | 1.8 | 3.831 | 4.7 | 1.41 | 8.5 | 2.709 | 0.0154 |
| D-026P | 0.25 | 1.2 | 0.7 | 1.8 | 4.015 | 6.6 | 2.18 | 12.5 | 1.842 | 0.0212 |
| D-026Q | 0.25 | 1.2 | 0.7 | 1.8 | 4.08 | 9.4 | 3.28 | 18.5 | 1.245 | 0.03 |
| D-026G | 0.25 | 1.6 | 1 | 2.2 | 3.078 | 3 | 1.11 | 3.5 | 2.776 | 0.0107 |
| D-026H | 0.25 | 1.6 | 1 | 2.2 | 3.229 | 4.3 | 1.83 | 5.5 | 1.766 | 0.0146 |
| D-026J | 0.25 | 1.6 | 1 | 2.2 | 3.266 | 6.2 | 2.86 | 8.5 | 1.143 | 0.0205 |
| D-026K | 0.25 | 1.6 | 1 | 2.2 | 3.261 | 8.7 | 4.2 | 12.5 | 0.777 | 0.0283 |
| D-026L | 0.25 | 1.6 | 1 | 2.2 | 3.284 | 12.5 | 6.25 | 18.5 | 0.525 | 0.04 |
| D-022A | 0.25 | 2 | 1.5 | 2.6 | 2.528 | 3.7 | 1.78 | 3.5 | 1.421 | 0.0134 |
| D-023A | 0.25 | 2 | 1.5 | 2.6 | 2.696 | 5.5 | 2.98 | 5.5 | 0.904 | 0.0183 |
| D-024A | 0.25 | 2 | 1.5 | 2.6 | 2.682 | 8 | 4.58 | 8.5 | 0.585 | 0.0256 |
| D-025A | 0.25 | 2 | 1.5 | 2.6 | 2.701 | 11.4 | 6.79 | 12.5 | 0.398 | 0.0354 |
| D-026A | 0.25 | 2 | 1.5 | 2.6 | 2.741 | 16.6 | 10.19 | 18.5 | 0.269 | 0.05 |
| D-017A | 0.25 | 2.5 | 1.9 | 3.1 | 2.133 | 4.9 | 2.93 | 3.5 | 0.728 | 0.0168 |
| D-018 | 0.25 | 2.5 | 1.9 | 3.1 | 2.179 | 7.3 | 4.71 | 5.5 | 0.463 | 0.0229 |
| D-019 | 0.25 | 2.5 | 1.9 | 3.1 | 2.208 | 10.9 | 7.37 | 8.5 | 0.3 | 0.032 |
| D-020A | 0.25 | 2.5 | 1.9 | 3.1 | 2.225 | 15.7 | 10.92 | 12.5 | 0.204 | 0.0442 |
| D-021A | 0.25 | 2.5 | 1.9 | 3.1 | 2.236 | 22.9 | 16.24 | 18.5 | 0.138 | 0.0625 |
| D-012A | 0.25 | 3.2 | 2.5 | 4 | 1.751 | 7.1 | 5.05 | 3.5 | 0.347 | 0.0215 |
| D-013A | 0.25 | 3.2 | 2.5 | 4 | 1.761 | 10.7 | 7.97 | 5.5 | 0.221 | 0.0293 |
| D-013B | 0.25 | 3.2 | 2.5 | 4 | 1.767 | 16.1 | 12.37 | 8.5 | 0.143 | 0.041 |
| D-015A | 0.25 | 3.2 | 2.5 | 4 | 1.77 | 23.3 | 18.22 | 12.5 | 0.097 | 0.0566 |
| D-016A | 0.25 | 3.2 | 2.5 | 4 | 1.772 | 34.1 | 27 | 18.5 | 0.066 | 0.08 |
| D-042F-01 | 0.32 | 1.6 | 1 | 2.2 | 5.261 | 3.1 | 0.71 | 3.5 | 7.451 | 0.0176 |
| D-042F-02 | 0.32 | 1.6 | 1 | 2.2 | 6.06 | 4.4 | 1.28 | 5.5 | 4.742 | 0.024 |
| D-042F-03 | 0.32 | 1.6 | 1 | 2.2 | 6.4 | 6.3 | 2.09 | 8.5 | 3.068 | 0.0336 |
| D-042F-04 | 0.32 | 1.6 | 1 | 2.2 | 6.322 | 8.7 | 3.03 | 12.5 | 2.086 | 0.0463 |
| D-042F-05 | 0.32 | 1.6 | 1 | 2.2 | 6.606 | 12.54 | 4.69 | 18.5 | 1.41 | 0.0655 |
| D-042B | 0.32 | 2 | 1.4 | 2.6 | 4.892 | 3.7 | 1.28 | 3.5 | 3.815 | 0.022 |
| D-042C | 0.32 | 2 | 1.4 | 2.6 | 5.198 | 5.3 | 2.14 | 5.5 | 2.428 | 0.03 |
| D-042D | 0.32 | 2 | 1.4 | 2.6 | 5.386 | 7.7 | 3.43 | 8.5 | 1.571 | 0.0419 |
| D-042E | 0.32 | 2 | 1.4 | 2.6 | 5.497 | 10.9 | 5.15 | 12.5 | 1.068 | 0.0579 |
| D-042F | 0.32 | 2 | 1.4 | 2.6 | 5.501 | 15.6 | 7.62 | 18.5 | 0.722 | 0.0819 |
| D-038A | 0.32 | 2.5 | 1.9 | 3.1 | 4.386 | 4.7 | 2.25 | 3.5 | 1.953 | 0.0275 |
| D-039A | 0.32 | 2.5 | 1.9 | 3.1 | 4.454 | 6.8 | 3.58 | 5.5 | 1.243 | 0.0374 |
| D-040A | 0.32 | 2.5 | 1.9 | 3.1 | 4.536 | 10 | 5.64 | 8.5 | 0.804 | 0.0524 |
| D-041A | 0.32 | 2.5 | 1.9 | 3.1 | 4.547 | 14.2 | 8.31 | 12.5 | 0.547 | 0.0724 |
| D-042A | 0.32 | 2.5 | 1.9 | 3.1 | 4.592 | 20.6 | 12.43 | 18.5 | 0.37 | 0.1024 |
| D-033A | 0.32 | 3.2 | 2.4 | 4 | 3.521 | 6.3 | 3.78 | 3.5 | 0.931 | 0.0352 |
| D-034A | 0.32 | 3.2 | 2.4 | 4 | 3.604 | 9.4 | 6.08 | 5.5 | 0.593 | 0.0479 |
| D-035A | 0.32 | 3.2 | 2.4 | 4 | 3.636 | 14 | 9.48 | 8.5 | 0.384 | 0.0671 |
| D-036A | 0.32 | 3.2 | 2.4 | 4 | 3.646 | 20.1 | 13.98 | 12.5 | 0.261 | 0.0927 |
| D-037A | 0.32 | 3.2 | 2.4 | 4 | 3.662 | 29.3 | 20.78 | 18.5 | 0.176 | 0.131 |
| D-028A | 0.32 | 4 | 3.2 | 4.8 | 2.902 | 8.7 | 6.09 | 3.5 | 0.477 | 0.0439 |
| D-029A | 0.32 | 4 | 3.2 | 4.8 | 2.923 | 13.1 | 9.63 | 5.5 | 0.303 | 0.0599 |
| D-030A | 0.32 | 4 | 3.2 | 4.8 | 1.782 | 19.8 | 13.34 | 12.5 | 0.134 | 0.1158 |
| D-030B | 0.32 | 4 | 3.2 | 4.8 | 2.957 | 28.6 | 22.14 | 12.5 | 0.134 | 0.1158 |
| D-032A | 0.32 | 4 | 3.2 | 4.8 | 2.967 | 41.9 | 32.88 | 18.5 | 0.09 | 0.1638 |
| D-063C | 0.4 | 2 | 1.3 | 2.7 | 8.453 | 3.9 | 0.91 | 3.5 | 9.314 | 0.0343 |
| D-063D | 0.4 | 2 | 1.3 | 2.7 | 9.469 | 5.5 | 1.6 | 5.5 | 5.927 | 0.0468 |
| D-063E | 0.4 | 2 | 1.3 | 2.7 | 9.713 | 7.8 | 2.53 | 8.5 | 3.835 | 0.0655 |
| D-063F | 0.4 | 2 | 1.3 | 2.7 | 9.943 | 10.9 | 3.81 | 12.5 | 2.608 | 0.0905 |
| D-063G | 0.4 | 2 | 1.3 | 2.7 | 10.19 | 15.6 | 5.78 | 18.5 | 1.762 | 0.1279 |
| D-059A | 0.4 | 2.5 | 1.8 | 3.2 | 8.002 | 4.7 | 1.68 | 3.5 | 4.769 | 0.0429 |
| D-060A | 0.4 | 2.5 | 1.8 | 3.2 | 8.349 | 6.7 | 2.75 | 5.5 | 3.035 | 0.0585 |
| D-061A | 0.4 | 2.5 | 1.8 | 3.2 | 8.367 | 9.6 | 4.26 | 8.5 | 1.964 | 0.0819 |
| D-062B | 0.4 | 2.5 | 1.8 | 3.2 | 8.555 | 13.6 | 6.41 | 12.5 | 1.335 | 0.1131 |
| D-063B | 0.4 | 2.5 | 1.8 | 3.2 | 8.595 | 19.5 | 9.53 | 18.5 | 0.902 | 0.1599 |
| D-053A | 0.4 | 3.2 | 2.5 | 4 | 6.653 | 6 | 2.93 | 3.5 | 2.274 | 0.0549 |
| D-054A | 0.4 | 3.2 | 2.5 | 4 | 6.756 | 8.7 | 4.67 | 5.5 | 1.447 | 0.0749 |
| D-055A | 0.4 | 3.2 | 2.5 | 4 | 6.867 | 12.8 | 7.33 | 8.5 | 0.936 | 0.1049 |
| D-056B | 0.4 | 3.2 | 2.5 | 4 | 6.953 | 18.3 | 10.92 | 12.5 | 0.637 | 0.1448 |
| D-057B | 0.4 | 3.2 | 2.5 | 4 | 6.991 | 26.5 | 16.25 | 18.5 | 0.43 | 0.2047 |
| D-048A | 0.4 | 4 | 3.2 | 4.9 | 5.53 | 7.9 | 4.75 | 3.5 | 1.164 | 0.0687 |
| D-049A | 0.4 | 4 | 3.2 | 4.9 | 5.594 | 11.7 | 7.55 | 5.5 | 0.741 | 0.0936 |
| D-050A | 0.4 | 4 | 3.2 | 4.9 | 5.681 | 17.5 | 11.85 | 8.5 | 0.479 | 0.1311 |
| D-051B | 0.4 | 4 | 3.2 | 4.9 | 5.689 | 25.1 | 17.45 | 12.5 | 0.326 | 0.181 |
| D-052B | 0.4 | 4 | 3.2 | 4.9 | 5.716 | 36.6 | 25.95 | 18.5 | 0.22 | 0.2559 |
| D-043A | 0.4 | 5 | 4.1 | 6 | 4.549 | 10.9 | 7.63 | 3.5 | 0.596 | 0.0858 |
| D-044A | 0.4 | 5 | 4.1 | 6 | 4.577 | 16.4 | 12.06 | 5.5 | 0.379 | 0.117 |
| D-045A | 0.4 | 5 | 4.1 | 6 | 4.606 | 24.7 | 18.76 | 8.5 | 0.245 | 0.1638 |
| D-046B | 0.4 | 5 | 4.1 | 6 | 4.628 | 35.8 | 27.73 | 12.5 | 0.167 | 0.2262 |
| D-047B | 0.4 | 5 | 4.1 | 6 | 4.638 | 52.4 | 41.13 | 18.5 | 0.113 | 0.3199 |
| D-086 | 0.5 | 2.5 | 1.7 | 3.3 | 16.409 | 4.4 | 1.41 | 3.5 | 11.643 | 0.067 |
| D-087 | 0.5 | 2.5 | 1.7 | 3.3 | 14.61 | 6.1 | 1.97 | 5.5 | 7.409 | 0.0914 |
| D-088 | 0.5 | 2.5 | 1.7 | 3.3 | 13.738 | 8.7 | 2.87 | 8.5 | 4.794 | 0.128 |
| D-089 | 0.5 | 2.5 | 1.7 | 3.3 | 12.683 | 12 | 3.89 | 12.5 | 3.26 | 0.1768 |
| D-090 | 0.5 | 2.5 | 1.7 | 3.3 | 13.168 | 17.5 | 5.98 | 18.5 | 2.203 | 0.2499 |
| D-081 | 0.5 | 3.2 | 2.4 | 4.1 | 13.699 | 5.5 | 2.47 | 3.5 | 5.552 | 0.0858 |
| D-082 | 0.5 | 3.2 | 2.4 | 4.1 | 13.093 | 7.9 | 3.71 | 5.5 | 3.533 | 0.117 |
| D-083 | 0.5 | 3.2 | 2.4 | 4.1 | 12.719 | 11.5 | 5.56 | 8.5 | 2.286 | 0.1638 |
| D-084 | 0.5 | 3.2 | 2.4 | 4.1 | 12.033 | 16 | 7.74 | 12.5 | 1.554 | 0.2262 |
| D-085 | 0.5 | 3.2 | 2.4 | 4.1 | 12.348 | 23.5 | 11.76 | 18.5 | 1.05 | 0.3199 |
| D-076 | 0.5 | 4 | 3.1 | 4.9 | 11.106 | 7 | 3.91 | 3.5 | 2.842 | 0.1073 |
| D-077 | 0.5 | 4 | 3.1 | 4.9 | 10.33 | 10 | 5.71 | 5.5 | 1.809 | 0.1463 |
| D-078 | 0.5 | 4 | 3.1 | 4.9 | 10.437 | 15 | 8.92 | 8.5 | 1.17 | 0.2048 |
| D-079 | 0.5 | 4 | 3.1 | 4.9 | 10.367 | 21.5 | 13.03 | 12.5 | 0.796 | 0.2828 |
| D-080 | 0.5 | 4 | 3.1 | 4.9 | 10.184 | 31 | 18.94 | 18.5 | 0.538 | 0.3998 |
| D-070 | 0.5 | 5 | 4.1 | 6.1 | 9.041 | 9.4 | 6.21 | 3.5 | 1.455 | 0.1341 |
| D-071 | 0.5 | 5 | 4.1 | 6.1 | 8.856 | 14 | 9.56 | 5.5 | 0.926 | 0.1828 |
| D-072 | 0.5 | 5 | 4.1 | 6.1 | 8.502 | 20.5 | 14.19 | 8.5 | 0.599 | 0.256 |
| D-073 | 0.5 | 5 | 4.1 | 6.1 | 8.634 | 30 | 21.19 | 12.5 | 0.408 | 0.3535 |
| D-074 | 0.5 | 5 | 4.1 | 6.1 | 8.794 | 44.5 | 31.94 | 18.5 | 0.275 | 0.4998 |
| D-064 | 0.5 | 6.3 | 5.4 | 7.5 | 7.391 | 13.5 | 10.16 | 3.5 | 0.728 | 0.169 |
| D-065 | 0.5 | 6.3 | 5.4 | 7.5 | 7.093 | 20 | 15.32 | 5.5 | 0.463 | 0.2304 |
| D-066 | 0.5 | 6.3 | 5.4 | 7.5 | 6.984 | 30 | 23.31 | 8.5 | 0.3 | 0.3225 |
| D-067 | 0.5 | 6.3 | 5.4 | 7.5 | 7.056 | 44 | 34.64 | 12.5 | 0.204 | 0.4454 |
| D-068 | 0.5 | 6.3 | 5.4 | 7.5 | 7.105 | 65 | 51.62 | 18.5 | 0.138 | 0.6297 |
| D-111 | 0.63 | 3.2 | 2.3 | 4.2 | 24.196 | 5.5 | 1.73 | 3.5 | 13.993 | 0.1362 |
| D-112 | 0.63 | 3.2 | 2.3 | 4.2 | 23.102 | 7.8 | 2.59 | 5.5 | 8.905 | 0.1858 |
| D-113 | 0.63 | 3.2 | 2.3 | 4.2 | 20.986 | 11 | 3.64 | 8.5 | 5.762 | 0.2601 |
| D-114 | 0.63 | 3.2 | 2.3 | 4.2 | 20.659 | 15.5 | 5.27 | 12.5 | 3.918 | 0.3592 |
| D-115 | 0.63 | 3.2 | 2.3 | 4.2 | 21.095 | 22.5 | 7.97 | 18.5 | 2.647 | 0.5078 |
| D-106 | 0.63 | 4 | 3 | 5 | 20.642 | 6.7 | 2.88 | 3.5 | 7.164 | 0.1703 |
| D-107 | 0.63 | 4 | 3 | 5 | 19.691 | 9.6 | 4.32 | 5.5 | 4.559 | 0.2322 |
| D-108 | 0.63 | 4 | 3 | 5 | 19.251 | 14 | 6.53 | 8.5 | 2.95 | 0.3251 |
| D-109 | 0.63 | 4 | 3 | 5 | 19.261 | 20 | 9.6 | 12.5 | 2.006 | 0.449 |
| D-110 | 0.63 | 4 | 3 | 5 | 19.267 | 29 | 14.21 | 18.5 | 1.355 | 0.6348 |
| D-101 | 0.63 | 5 | 4 | 6.1 | 16.896 | 8.5 | 4.61 | 3.5 | 3.668 | 0.2129 |
| D-102 | 0.63 | 5 | 4 | 6.1 | 16.576 | 12.5 | 7.1 | 5.5 | 2.334 | 0.2903 |
| D-103 | 0.63 | 5 | 4 | 6.1 | 16.378 | 18.5 | 10.84 | 8.5 | 1.51 | 0.4064 |
| D-104 | 0.63 | 5 | 4 | 6.1 | 15.749 | 26 | 15.33 | 12.5 | 1.027 | 0.5612 |
| D-105 | 0.63 | 5 | 4 | 6.1 | 16.182 | 38.5 | 23.32 | 18.5 | 0.694 | 0.7935 |
| D-096 | 0.63 | 6.3 | 5.2 | 7.5 | 13.723 | 11.5 | 7.48 | 3.5 | 1.834 | 0.2682 |
| D-097 | 0.63 | 6.3 | 5.2 | 7.5 | 13.313 | 17 | 11.41 | 5.5 | 1.167 | 0.3658 |
| D-098 | 0.63 | 6.3 | 5.2 | 7.5 | 13.249 | 25.5 | 17.55 | 8.5 | 0.755 | 0.5121 |
| D-099 | 0.63 | 6.3 | 5.2 | 7.5 | 13.04 | 36.5 | 25.4 | 12.5 | 0.513 | 0.7071 |
| D-100 | 0.63 | 6.3 | 5.2 | 7.5 | 13.243 | 54 | 38.17 | 18.5 | 0.347 | 0.9998 |
| D-091 | 0.63 | 8 | 6.9 | 9.4 | 10.551 | 16 | 11.78 | 3.5 | 0.896 | 0.3406 |
| D-092 | 0.63 | 8 | 6.9 | 9.4 | 10.595 | 24.5 | 18.59 | 5.5 | 0.57 | 0.4645 |
| D-093 | 0.63 | 8 | 6.9 | 9.4 | 10.53 | 37 | 28.55 | 8.5 | 0.369 | 0.6503 |
| D-094 | 0.63 | 8 | 6.9 | 9.4 | 10.826 | 55 | 43.17 | 12.5 | 0.251 | 0.898 |
| D-095 | 0.63 | 8 | 6.9 | 9.4 | 10.776 | 80.5 | 63.6 | 18.5 | 0.169 | 1.2695 |
| D-138 | 0.8 | 4 | 2.8 | 5.2 | 39.399 | 6.9 | 2.12 | 3.5 | 18.629 | 0.2746 |
| D-139 | 0.8 | 4 | 2.8 | 5.2 | 36.69 | 9.7 | 3.1 | 5.5 | 11.855 | 0.3745 |
| D-140 | 0.8 | 4 | 2.8 | 5.2 | 35.783 | 14 | 4.67 | 8.5 | 7.671 | 0.5243 |
| D-141 | 0.8 | 4 | 2.8 | 5.2 | 34.034 | 19.5 | 6.53 | 12.5 | 5.216 | 0.724 |
| D-142 | 0.8 | 4 | 2.8 | 5.2 | 33.71 | 28 | 9.57 | 18.5 | 3.524 | 1.0236 |
| D-133 | 0.8 | 5 | 3.8 | 6.3 | 32.962 | 8.3 | 3.46 | 3.5 | 9.538 | 0.3433 |
| D-134 | 0.8 | 5 | 3.8 | 6.3 | 32.182 | 12 | 5.3 | 5.5 | 6.07 | 0.4681 |
| D-135 | 0.8 | 5 | 3.8 | 6.3 | 31.503 | 17.5 | 8.02 | 8.5 | 3.927 | 0.6553 |
| D-136 | 0.8 | 5 | 3.8 | 6.3 | 30.215 | 24.5 | 11.31 | 12.5 | 2.671 | 0.905 |
| D-137 | 0.8 | 5 | 3.8 | 6.3 | 31.132 | 36 | 17.25 | 18.5 | 1.804 | 1.2795 |
| D-128 | 0.8 | 6.3 | 5.1 | 7.6 | 26.508 | 10.5 | 5.56 | 3.5 | 4.768 | 0.4325 |
| D-129 | 0.8 | 6.3 | 5.1 | 7.6 | 26.248 | 15.5 | 8.65 | 5.5 | 3.034 | 0.5898 |
| D-130 | 0.8 | 6.3 | 5.1 | 7.6 | 26.087 | 23 | 13.29 | 8.5 | 1.963 | 0.8257 |
| D-131 | 0.8 | 6.3 | 5.1 | 7.6 | 25.993 | 33 | 19.47 | 12.5 | 1.335 | 1.1403 |
| D-132 | 0.8 | 6.3 | 5.1 | 7.6 | 25.928 | 48 | 28.74 | 18.5 | 0.902 | 1.6121 |
| D-123 | 0.8 | 8 | 6.7 | 9.5 | 21.889 | 14.5 | 9.4 | 3.5 | 2.329 | 0.5492 |
| D-124 | 0.8 | 8 | 6.7 | 9.5 | 21.338 | 21.5 | 14.4 | 5.5 | 1.482 | 0.7489 |
| D-125 | 0.8 | 8 | 6.7 | 9.5 | 20.998 | 32 | 21.9 | 8.5 | 0.959 | 1.0485 |
| D-126 | 0.8 | 8 | 6.7 | 9.5 | 21.451 | 47 | 32.9 | 12.5 | 0.652 | 1.448 |
| D-127 | 0.8 | 8 | 6.7 | 9.5 | 21.102 | 68 | 47.9 | 18.5 | 0.441 | 2.0471 |
| D-118 | 0.8 | 10 | 8.7 | 11.6 | 17.483 | 20 | 14.66 | 3.5 | 1.192 | 0.6865 |
| D-119 | 0.8 | 10 | 8.7 | 11.6 | 17.092 | 30 | 22.53 | 5.5 | 0.759 | 0.9362 |
| D-120 | 0.8 | 10 | 8.7 | 11.6 | 17.136 | 45.58 | 34.91 | 8.5 | 0.491 | 1.3107 |
| D-121 | 0.8 | 10 | 8.7 | 11.6 | 17.044 | 66 | 51.06 | 12.5 | 0.334 | 1.81 |
| D-122 | 0.8 | 10 | 8.7 | 11.6 | 16.951 | 96.5 | 75.15 | 18.5 | 0.226 | 2.5589 |
| D-174 | 1 | 5 | 3.6 | 6.4 | 58.651 | 8.5 | 2.52 | 3.5 | 23.286 | 0.5364 |
| D-175 | 1 | 5 | 3.6 | 6.4 | 55.476 | 12 | 3.74 | 5.5 | 14.818 | 0.7314 |
| D-176 | 1 | 5 | 3.6 | 6.4 | 51.117 | 17 | 5.33 | 8.5 | 9.588 | 1.024 |
| D-177 | 1 | 5 | 3.6 | 6.4 | 50.734 | 24 | 7.78 | 12.5 | 6.52 | 1.414 |
| D-178 | 1 | 5 | 3.6 | 6.4 | 48.267 | 34 | 10.96 | 18.5 | 4.405 | 1.9991 |
| D-167 | 1 | 6.3 | 4.9 | 7.8 | 45.883 | 10 | 3.94 | 3.5 | 11.641 | 0.6758 |
| D-168 | 1 | 6.3 | 4.9 | 7.8 | 45.354 | 14.5 | 6.12 | 5.5 | 7.408 | 0.9216 |
| D-169 | 1 | 6.3 | 4.9 | 7.8 | 46.226 | 21.5 | 9.64 | 8.5 | 4.793 | 1.2902 |
| D-170 | 1 | 6.3 | 4.9 | 7.8 | 45.65 | 30.5 | 14.01 | 12.5 | 3.259 | 1.7817 |
| D-171 | 1 | 6.3 | 4.9 | 7.8 | 44.153 | 43.5 | 20.05 | 18.5 | 2.202 | 2.5189 |
| D-159 | 1 | 8 | 6.5 | 9.6 | 38.738 | 13 | 6.81 | 3.5 | 5.685 | 0.8582 |
| D-160 | 1 | 8 | 6.5 | 9.6 | 37.704 | 19 | 10.42 | 5.5 | 3.618 | 1.1702 |
| D-161 | 1 | 8 | 6.5 | 9.6 | 38.236 | 28.5 | 16.33 | 8.5 | 2.341 | 1.6383 |
| D-163 | 1 | 8 | 6.5 | 9.6 | 37.487 | 40.5 | 23.55 | 12.5 | 1.592 | 2.2624 |
| D-165 | 1 | 8 | 6.5 | 9.6 | 37.508 | 59 | 34.87 | 18.5 | 1.076 | 3.1986 |
| D-151 | 1 | 10 | 8.5 | 11.7 | 32.382 | 17.5 | 11.13 | 3.5 | 2.911 | 1.0727 |
| D-152 | 1 | 10 | 8.5 | 11.7 | 31.72 | 26 | 17.13 | 5.5 | 1.852 | 1.4628 |
| D-153 | 1 | 10 | 8.5 | 11.7 | 31.611 | 39 | 26.38 | 8.5 | 1.199 | 2.0479 |
| D-154 | 1 | 10 | 8.5 | 11.7 | 31.276 | 56 | 38.38 | 12.5 | 0.815 | 2.8281 |
| D-155 | 1 | 10 | 8.5 | 11.7 | 31.044 | 81.5 | 56.38 | 18.5 | 0.551 | 3.9983 |
| D-146 | 1 | 12.5 | 10.9 | 14.3 | 25.826 | 24 | 17.33 | 3.5 | 1.49 | 1.3409 |
| D-147 | 1 | 12.5 | 10.9 | 14.3 | 25.758 | 36.5 | 27.16 | 5.5 | 0.948 | 1.8285 |
| D-148 | 1 | 12.5 | 10.9 | 14.3 | 25.87 | 55.5 | 42.16 | 8.5 | 0.614 | 2.5599 |
| D-149 | 1 | 12.5 | 10.9 | 14.3 | 25.796 | 80.5 | 61.82 | 12.5 | 0.417 | 3.5351 |
| D-150 | 1 | 12.5 | 10.9 | 14.3 | 24.9 | 115 | 88.31 | 18.5 | 0.282 | 4.9979 |
| D-201 | 1.25 | 6.3 | 4.6 | 8.1 | 128.479 | 12 | 4.52 | 3.5 | 28.42 | 1.056 |
| D-202 | 1.25 | 6.3 | 4.6 | 8.1 | 120.729 | 17 | 6.68 | 5.5 | 18.085 | 1.4399 |
| D-203 | 1.25 | 6.3 | 4.6 | 8.1 | 121.792 | 25 | 10.41 | 8.5 | 11.702 | 2.0159 |
| D-204 | 1.25 | 6.3 | 4.6 | 8.1 | 121.09 | 35.5 | 15.22 | 12.5 | 7.957 | 2.7839 |
| D-205 | 1.25 | 6.3 | 4.6 | 8.1 | 121.951 | 51.5 | 22.68 | 18.5 | 5.377 | 3.9358 |
| D-196 | 1.25 | 8 | 6.3 | 9.8 | 102.967 | 15 | 7.42 | 3.5 | 13.879 | 1.3409 |
| D-197 | 1.25 | 8 | 6.3 | 9.8 | 101.705 | 22 | 11.52 | 5.5 | 8.832 | 1.8285 |
| D-198 | 1.25 | 8 | 6.3 | 9.8 | 103.156 | 33 | 18.05 | 8.5 | 5.715 | 2.5599 |
| D-199 | 1.25 | 8 | 6.3 | 9.8 | 103.179 | 47.5 | 26.55 | 12.5 | 3.886 | 3.5351 |
| D-200 | 1.25 | 8 | 6.3 | 9.8 | 103.064 | 69 | 39.25 | 18.5 | 2.626 | 4.9979 |
| D-191 | 1.25 | 10 | 8.3 | 11.9 | 82.788 | 20 | 11.65 | 3.5 | 7.106 | 1.6761 |
| D-192 | 1.25 | 10 | 8.3 | 11.9 | 82.755 | 29.5 | 18.3 | 5.5 | 4.522 | 2.2856 |
| D-193 | 1.25 | 10 | 8.3 | 11.9 | 82.809 | 44.5 | 28.3 | 8.5 | 2.926 | 3.1998 |
| D-194 | 1.25 | 10 | 8.3 | 11.9 | 82.773 | 64 | 41.6 | 12.5 | 1.99 | 4.4188 |
| D-195 | 1.25 | 10 | 8.3 | 11.9 | 82.816 | 93.5 | 61.6 | 18.5 | 1.344 | 6.2473 |
| D-186 | 1.25 | 12.5 | 10.7 | 14.6 | 66.219 | 27 | 18.2 | 3.5 | 3.638 | 2.0951 |
| D-187 | 1.25 | 12.5 | 10.7 | 14.6 | 66.219 | 41.5 | 28.6 | 5.5 | 2.315 | 2.857 |
| D-188 | 1.25 | 12.5 | 10.7 | 14.6 | 66.369 | 62.5 | 44.3 | 8.5 | 1.498 | 3.9998 |
| D-189 | 1.25 | 12.5 | 10.7 | 14.6 | 66.219 | 90.5 | 65 | 12.5 | 1.019 | 5.5235 |
| D-190 | 1.25 | 12.5 | 10.7 | 14.6 | 66.425 | 130 | 96.5 | 18.5 | 0.688 | 7.8092 |
| D-181 | 1.25 | 16 | 14.2 | 18.5 | 51.701 | 40.5 | 29.8 | 3.5 | 1.735 | 2.6818 |
| D-182 | 1.25 | 16 | 14.2 | 18.5 | 51.945 | 62 | 47.05 | 5.5 | 1.104 | 3.657 |
| D-183 | 1.25 | 16 | 14.2 | 18.5 | 51.9 | 94 | 72.65 | 8.5 | 0.714 | 5.1198 |
| D-184 | 1.25 | 16 | 14.2 | 18.5 | 51.881 | 140 | 106.8 | 12.5 | 0.486 | 7.0701 |
| D-185 | 1.25 | 16 | 14.2 | 18.5 | 52.024 | 205 | 158.5 | 18.5 | 0.328 | 9.9957 |
| D-228 | 1.6 | 8 | 5.9 | 10.1 | 183.678 | 14.5 | 4.93 | 3.5 | 37.257 | 2.1969 |
| D-229 | 1.6 | 8 | 5.9 | 10.1 | 196.548 | 21.5 | 8.29 | 5.5 | 23.709 | 2.9958 |
| D-230 | 1.6 | 8 | 5.9 | 10.1 | 196.827 | 31.5 | 12.83 | 8.5 | 15.341 | 4.1941 |
| D-231 | 1.6 | 8 | 5.9 | 10.1 | 198.73 | 45 | 19.05 | 12.5 | 10.432 | 5.7919 |
| D-232 | 1.6 | 8 | 5.9 | 10.1 | 201.803 | 65.5 | 28.63 | 18.5 | 7.049 | 8.1885 |
| D-223 | 1.6 | 10 | 7.9 | 12.2 | 165.958 | 18.5 | 8.7 | 3.5 | 19.076 | 2.7461 |
| D-224 | 1.6 | 10 | 7.9 | 12.2 | 165.144 | 27 | 13.6 | 5.5 | 12.139 | 3.7447 |
| D-225 | 1.6 | 10 | 7.9 | 12.2 | 166.362 | 40.5 | 21.18 | 8.5 | 7.855 | 5.2426 |
| D-226 | 1.6 | 10 | 7.9 | 12.2 | 167.179 | 58.5 | 31.3 | 12.5 | 5.341 | 7.2398 |
| D-227 | 1.6 | 10 | 7.9 | 12.2 | 166.01 | 85 | 46 | 18.5 | 3.609 | 10.2356 |
| D-218 | 1.6 | 12.5 | 10.4 | 14.7 | 133.316 | 24 | 13.65 | 3.5 | 9.767 | 3.4327 |
| D-219 | 1.6 | 12.5 | 10.4 | 14.7 | 133.316 | 36 | 21.45 | 5.5 | 6.215 | 4.6809 |
| D-220 | 1.6 | 12.5 | 10.4 | 14.7 | 133.517 | 53.5 | 33.2 | 8.5 | 4.022 | 6.5533 |
| D-221 | 1.6 | 12.5 | 10.4 | 14.7 | 133.179 | 78 | 48.7 | 12.5 | 2.735 | 9.0498 |
| D-222 | 1.6 | 12.5 | 10.4 | 14.7 | 133.408 | 115 | 72.2 | 18.5 | 1.848 | 12.7945 |
| D-213 | 1.6 | 16 | 13.8 | 18.6 | 104.087 | 34 | 22.35 | 3.5 | 4.657 | 4.3938 |
| D-214 | 1.6 | 16 | 13.8 | 18.6 | 104.172 | 51.1 | 35.15 | 5.5 | 2.964 | 5.9916 |
| D-215 | 1.6 | 16 | 13.8 | 18.6 | 103.841 | 77.5 | 54.15 | 8.5 | 1.918 | 8.3882 |
| D-216 | 1.6 | 16 | 13.8 | 18.6 | 104.19 | 110 | 79.9 | 12.5 | 1.304 | 11.5837 |
| D-217 | 1.6 | 16 | 13.8 | 18.6 | 104.056 | 165 | 118.1 | 18.5 | 0.881 | 16.377 |
| D-208 | 1.6 | 20 | 17.7 | 23 | 83.218 | 48 | 34.9 | 3.5 | 2.384 | 5.4923 |
| D-209 | 1.6 | 20 | 17.7 | 23 | 83.304 | 73.5 | 54.9 | 5.5 | 1.517 | 7.4895 |
| D-210 | 1.6 | 20 | 17.7 | 23 | 83.358 | 110 | 84.9 | 8.5 | 0.982 | 10.4853 |
| D-211 | 1.6 | 20 | 17.7 | 23 | 83.122 | 165 | 124.5 | 12.5 | 0.668 | 14.4797 |
| D-212 | 1.6 | 20 | 17.7 | 23 | 83.321 | 240 | 184.7 | 18.5 | 0.451 | 20.4712 |
| D-258 | 2 | 10 | 7.5 | 12.6 | 281.175 | 18 | 6.04 | 3.5 | 46.571 | 4.2908 |
| D-259 | 2 | 10 | 7.5 | 12.6 | 295.993 | 26.5 | 9.99 | 5.5 | 29.636 | 5.8512 |
| D-260 | 2 | 10 | 7.5 | 12.6 | 290.763 | 38.5 | 15.16 | 8.5 | 19.176 | 8.1916 |
| D-261 | 2 | 10 | 7.5 | 12.6 | 294.215 | 55 | 22.56 | 12.5 | 13.04 | 11.3122 |
| D-262 | 2 | 10 | 7.5 | 12.6 | 294.391 | 79.5 | 33.41 | 18.5 | 8.811 | 15.9932 |
| D-253 | 2 | 12.5 | 10 | 15.2 | 247.741 | 22.5 | 10.39 | 3.5 | 23.845 | 5.3636 |
| D-254 | 2 | 12.5 | 10 | 15.2 | 246.658 | 33 | 16.26 | 5.5 | 15.174 | 7.3139 |
| D-255 | 2 | 12.5 | 10 | 15.2 | 250.368 | 49.5 | 25.5 | 8.5 | 9.818 | 10.2395 |
| D-256 | 2 | 12.5 | 10 | 15.2 | 250.368 | 71 | 37.5 | 12.5 | 6.676 | 14.1403 |
| D-257 | 2 | 12.5 | 10 | 15.2 | 250.368 | 105 | 55.5 | 18.5 | 4.511 | 19.9914 |
| D-248 | 2 | 16 | 13.5 | 18.6 | 195.564 | 30 | 17.2 | 3.5 | 11.37 | 6.8654 |
| D-249 | 2 | 16 | 13.5 | 18.6 | 195.357 | 45 | 27 | 5.5 | 7.235 | 9.3618 |
| D-250 | 2 | 16 | 13.5 | 18.6 | 194.995 | 68 | 41.65 | 8.5 | 4.682 | 13.1066 |
| D-251 | 2 | 16 | 13.5 | 18.6 | 195.313 | 98 | 61.35 | 12.5 | 3.184 | 18.0996 |
| D-252 | 2 | 16 | 13.5 | 18.6 | 195.21 | 145 | 90.75 | 18.5 | 2.151 | 25.589 |
| D-240 | 2 | 20 | 17.3 | 23.1 | 156.014 | 41 | 26.8 | 3.5 | 5.821 | 8.5817 |
| D-241 | 2 | 20 | 17.3 | 23.1 | 156.147 | 62 | 42.15 | 5.5 | 3.705 | 11.7023 |
| D-242 | 2 | 20 | 17.3 | 23.1 | 156.288 | 94 | 65.2 | 8.5 | 2.397 | 16.3832 |
| D-243 | 2 | 20 | 17.3 | 23.1 | 156.48 | 135 | 96 | 12.5 | 1.63 | 22.6245 |
| D-244 | 2 | 20 | 17.3 | 23.1 | 156.557 | 200 | 142.15 | 18.5 | 1.101 | 31.9863 |
| D-235 | 2 | 25 | 22.3 | 28.6 | 125.184 | 58 | 42 | 3.5 | 2.981 | 10.7271 |
| D-236 | 2 | 25 | 22.3 | 28.6 | 125.184 | 88.5 | 66 | 5.5 | 1.897 | 14.6279 |
| D-237 | 2 | 25 | 22.3 | 28.6 | 125.245 | 135 | 102.05 | 8.5 | 1.227 | 20.479 |
| D-238 | 2 | 25 | 22.3 | 28.6 | 125.184 | 195 | 150 | 12.5 | 0.835 | 28.2806 |
| D-239 | 2 | 25 | 22.3 | 28.6 | 125.212 | 290 | 222.05 | 18.5 | 0.564 | 39.9829 |
| D-284 | 2.5 | 12.5 | 9.4 | 15.7 | 410.229 | 22 | 7.05 | 3.5 | 58.214 | 8.3806 |
| D-285 | 2.5 | 12.5 | 9.4 | 15.7 | 420.813 | 32 | 11.36 | 5.5 | 37.045 | 11.428 |
| D-286 | 2.5 | 12.5 | 9.4 | 15.7 | 439.336 | 47.5 | 18.33 | 8.5 | 23.971 | 15.9992 |
| D-287 | 2.5 | 12.5 | 9.4 | 15.7 | 439.336 | 67.5 | 26.95 | 12.5 | 16.3 | 22.0942 |
| D-288 | 2.5 | 12.5 | 9.4 | 15.7 | 444.843 | 98 | 40.39 | 18.5 | 11.014 | 31.2366 |
| D-279 | 2.5 | 16 | 12.9 | 19.3 | 342.471 | 27.5 | 12.34 | 3.5 | 27.759 | 10.7271 |
| D-280 | 2.5 | 16 | 12.9 | 19.3 | 353.826 | 41 | 20.03 | 5.5 | 17.665 | 14.6279 |
| D-281 | 2.5 | 16 | 12.9 | 19.3 | 357.983 | 61 | 31.32 | 8.5 | 11.43 | 20.479 |
| D-282 | 2.5 | 16 | 12.9 | 19.3 | 363.012 | 88 | 46.71 | 12.5 | 7.772 | 28.2806 |
| D-283 | 2.5 | 16 | 12.9 | 19.3 | 366.04 | 130 | 69.7 | 18.5 | 5.252 | 39.9829 |
| D-274 | 2.5 | 20 | 16.8 | 23.3 | 291.853 | 36 | 20.54 | 3.5 | 14.212 | 13.4089 |
| D-275 | 2.5 | 20 | 16.8 | 23.3 | 292.131 | 54 | 32.3 | 5.5 | 9.044 | 18.2849 |
| D-276 | 2.5 | 20 | 16.8 | 23.3 | 292.61 | 81.5 | 50 | 8.5 | 5.852 | 25.5988 |
| D-277 | 2.5 | 20 | 16.8 | 23.3 | 293.289 | 120 | 73.7 | 12.5 | 3.979 | 35.3507 |
| D-278 | 2.5 | 20 | 16.8 | 23.3 | 292.546 | 175 | 108.8 | 18.5 | 2.689 | 49.9786 |
| D-269 | 2.5 | 25 | 21.8 | 28.8 | 234.313 | 49 | 32.2 | 3.5 | 7.277 | 16.7611 |
| D-270 | 2.5 | 25 | 21.8 | 28.8 | 233.849 | 74.5 | 50.5 | 5.5 | 4.631 | 22.8561 |
| D-271 | 2.5 | 25 | 21.8 | 28.8 | 233.713 | 115 | 78 | 8.5 | 2.996 | 31.9985 |
| D-272 | 2.5 | 25 | 21.8 | 28.8 | 234.72 | 165 | 115.2 | 12.5 | 2.038 | 44.1884 |
| D-273 | 2.5 | 25 | 21.8 | 28.8 | 235.001 | 240 | 170.7 | 18.5 | 1.377 | 62.4732 |
| D-264 | 2.5 | 32 | 28.7 | 35.3 | 182.514 | 71.5 | 52.6 | 3.5 | 3.47 | 21.4542 |
| D-265 | 2.5 | 32 | 28.7 | 35.3 | 183.271 | 110 | 83 | 5.5 | 2.208 | 29.2558 |
| D-266 | 2.5 | 32 | 28.7 | 35.3 | 182.881 | 170 | 128 | 8.5 | 1.429 | 40.9581 |
| D-267 | 2.5 | 32 | 28.7 | 35.3 | 182.652 | 245 | 188 | 12.5 | 0.972 | 56.5611 |
| D-268 | 2.5 | 32 | 28.7 | 35.5 | 183.283 | 360 | 279.2 | 18.5 | 0.656 | 79.9658 |
| D-309 | 3.2 | 16 | 12.1 | 20.1 | 622.939 | 27.5 | 8.36 | 3.5 | 74.514 | 17.5753 |
| D-310 | 3.2 | 16 | 12.1 | 20.1 | 643.939 | 40 | 13.58 | 5.5 | 47.418 | 23.9663 |
| D-311 | 3.2 | 16 | 12.1 | 20.1 | 664.58 | 59 | 21.66 | 8.5 | 30.682 | 33.5529 |
| D-312 | 3.2 | 16 | 12.1 | 20.1 | 659.302 | 83.5 | 31.6 | 12.5 | 20.864 | 46.3349 |
| D-313 | 3.2 | 16 | 12.1 | 20.1 | 652.141 | 120 | 46.26 | 18.5 | 14.097 | 65.5079 |
| D-304 | 3.2 | 20 | 16.1 | 24.2 | 538.84 | 33.5 | 14.12 | 3.5 | 38.151 | 21.9691 |
| D-305 | 3.2 | 20 | 16.1 | 24.2 | 551.326 | 49.5 | 22.71 | 5.5 | 24.278 | 29.9579 |
| D-306 | 3.2 | 20 | 16.1 | 24.2 | 566.892 | 74 | 36.09 | 8.5 | 15.709 | 41.9411 |
| D-307 | 3.2 | 20 | 16.1 | 24.2 | 558.22 | 105 | 52.26 | 12.5 | 10.682 | 57.9186 |
| D-308 | 3.2 | 20 | 16.1 | 24.2 | 577.506 | 155 | 80.01 | 18.5 | 7.218 | 81.8849 |
| D-299 | 3.2 | 25 | 21 | 29.3 | 444.477 | 42.5 | 22.75 | 3.5 | 19.533 | 27.4614 |
| D-300 | 3.2 | 25 | 21 | 29.3 | 449.094 | 63.5 | 36.13 | 5.5 | 12.43 | 37.4474 |
| D-301 | 3.2 | 25 | 21 | 29.3 | 447.924 | 94.5 | 55.69 | 8.5 | 8.043 | 52.4263 |
| D-302 | 3.2 | 25 | 21 | 29.3 | 442.679 | 135 | 80.94 | 12.5 | 5.469 | 72.3983 |
| D-303 | 3.2 | 25 | 21 | 29.3 | 454.771 | 200 | 123.06 | 18.5 | 3.696 | 102.3562 |
| D-294 | 3.2 | 32 | 27.8 | 36.9 | 354.874 | 58.5 | 38.1 | 3.5 | 9.314 | 35.1506 |
| D-295 | 3.2 | 32 | 27.8 | 36.9 | 356.229 | 88.5 | 60.1 | 5.5 | 5.927 | 47.9326 |
| D-296 | 3.2 | 32 | 27.8 | 36.9 | 362.819 | 135 | 94.6 | 8.5 | 3.835 | 67.1057 |
| D-297 | 3.2 | 32 | 27.8 | 36.9 | 348.429 | 190 | 133.6 | 12.5 | 2.608 | 92.6698 |
| D-298 | 3.2 | 32 | 27.8 | 36.9 | 351.728 | 280 | 199.6 | 18.5 | 1.762 | 131.0159 |
| D-289D | 3.2 | 40 | 35.8 | 45.3 | 289.258 | 82 | 60.66 | 3.5 | 4.769 | 43.9383 |
| D-290 | 3.2 | 40 | 35.8 | 45.3 | 288.652 | 125 | 95.12 | 5.5 | 3.035 | 59.9158 |
| D-291 | 3.2 | 40 | 35.8 | 45.3 | 289.258 | 190 | 147.31 | 8.5 | 1.964 | 83.8821 |
| D-292 | 3.2 | 40 | 35.8 | 45.3 | 287.389 | 275 | 215.23 | 12.5 | 1.335 | 115.8372 |
| D-293 | 3.2 | 40 | 35.8 | 45.3 | 288.356 | 405 | 319.61 | 18.5 | 0.902 | 163.7699 |
| D-335 | 4 | 20 | 15.2 | 25.1 | 891.843 | 33.5 | 9.58 | 3.5 | 93.143 | 34.3268 |
| D-336 | 4 | 20 | 15.2 | 25.1 | 946.882 | 49 | 15.98 | 5.5 | 59.273 | 46.8092 |
| D-337 | 4 | 20 | 15.2 | 25.1 | 971.288 | 72 | 25.33 | 8.5 | 38.353 | 65.5329 |
| D-338 | 4 | 20 | 15.2 | 25.1 | 1046.46 | 105 | 40.13 | 12.5 | 26.08 | 90.4978 |
| D-339 | 4 | 20 | 15.2 | 25.1 | 1018.97 | 150 | 57.83 | 18.5 | 17.622 | 127.9452 |
| D-330 | 4 | 25 | 20.3 | 30 | 800.209 | 41 | 16.78 | 3.5 | 47.689 | 42.9085 |
| D-331 | 4 | 25 | 20.3 | 30 | 819.718 | 60.5 | 27.01 | 5.5 | 30.348 | 58.5115 |
| D-332 | 4 | 25 | 20.3 | 30 | 826.859 | 89.5 | 42.11 | 8.5 | 19.637 | 81.9161 |
| D-333 | 4 | 25 | 20.3 | 30 | 855.528 | 130 | 64.07 | 12.5 | 13.353 | 113.1223 |
| D-334 | 4 | 25 | 20.3 | 30 | 823.409 | 185 | 91.26 | 18.5 | 9.022 | 159.9315 |
| D-325 | 4 | 32 | 27.1 | 37.1 | 653.91 | 53.5 | 28.76 | 3.5 | 22.74 | 54.9228 |
| D-326 | 4 | 32 | 27.1 | 37.1 | 653.91 | 79.5 | 45.19 | 5.5 | 14.471 | 74.8948 |
| D-327 | 4 | 32 | 27.1 | 37.1 | 667.955 | 120 | 71.34 | 8.5 | 9.364 | 104.8527 |
| D-328 | 4 | 32 | 27.1 | 37.1 | 650.727 | 170 | 102.2 | 12.5 | 6.367 | 144.7965 |
| D-329 | 4 | 32 | 27.1 | 37.1 | 660.363 | 250 | 153.5 | 18.5 | 4.302 | 204.7123 |
| D-319 | 4 | 40 | 34.9 | 45.8 | 529.75 | 71 | 45.5 | 3.5 | 11.643 | 68.6535 |
| D-320 | 4 | 40 | 34.9 | 45.8 | 514.932 | 105 | 69.5 | 5.5 | 7.409 | 93.6184 |
| D-321 | 4 | 40 | 34.9 | 45.8 | 524.956 | 160 | 109.5 | 8.5 | 4.794 | 131.0658 |
| D-322 | 4 | 40 | 34.9 | 45.8 | 536.27 | 235 | 164.5 | 12.5 | 3.26 | 180.9957 |
| D-323 | 4 | 40 | 34.9 | 45.8 | 527.547 | 340 | 239.5 | 18.5 | 2.203 | 255.8904 |
| D-314 | 4 | 50 | 44.8 | 56.2 | 431.102 | 99 | 72.32 | 3.5 | 5.961 | 85.8169 |
| D-315 | 4 | 50 | 44.8 | 56.2 | 427.309 | 150 | 112.64 | 5.5 | 3.793 | 117.0231 |
| D-316 | 4 | 50 | 44.8 | 56.2 | 433.557 | 230 | 176.63 | 8.5 | 2.455 | 163.8323 |
| D-317 | 4 | 50 | 44.8 | 56.2 | 434.441 | 335 | 260.28 | 12.5 | 1.669 | 226.2446 |
| D-318 | 4 | 50 | 44.8 | 56.2 | 432.23 | 490 | 383.26 | 18.5 | 1.128 | 319.863 |
| D-360 | 5 | 25 | 19.1 | 31 | 1291.629 | 41 | 11.09 | 3.5 | 116.429 | 67.0445 |
| D-361 | 5 | 25 | 19.1 | 31 | 1386.889 | 60 | 18.72 | 5.5 | 74.091 | 91.4243 |
| D-362 | 5 | 25 | 19.1 | 31 | 1397.785 | 87.5 | 29.16 | 8.5 | 47.941 | 127.994 |
| D-363 | 5 | 25 | 19.1 | 31 | 1431.344 | 125 | 43.91 | 12.5 | 32.6 | 176.7536 |
| D-364 | 5 | 25 | 19.1 | 31 | 1426.938 | 180 | 64.78 | 18.5 | 22.027 | 249.893 |
| D-355 | 5 | 32 | 26 | 38.2 | 1147.813 | 51 | 20.67 | 3.5 | 55.517 | 85.8169 |
| D-356 | 5 | 32 | 26 | 38.2 | 1168.001 | 75 | 33.06 | 5.5 | 35.329 | 117.0231 |
| D-357 | 5 | 32 | 26 | 38.2 | 1157.61 | 110 | 50.64 | 8.5 | 22.86 | 163.8323 |
| D-358 | 5 | 32 | 26 | 38.2 | 1203.33 | 160 | 77.41 | 12.5 | 15.545 | 226.2446 |
| D-359 | 5 | 32 | 26 | 38.2 | 1182.323 | 230 | 112.57 | 18.5 | 10.503 | 319.863 |
| D-350 | 5 | 40 | 34 | 46.5 | 940.013 | 64 | 33.07 | 3.5 | 28.425 | 107.2711 |
| D-351 | 5 | 40 | 34 | 46.5 | 951.641 | 95.5 | 52.61 | 5.5 | 18.089 | 146.2788 |
| D-352 | 5 | 40 | 34 | 46.5 | 926.636 | 140 | 79.17 | 8.5 | 11.704 | 204.7904 |
| D-353 | 5 | 40 | 34 | 46.5 | 957.068 | 205 | 120.25 | 12.5 | 7.959 | 282.8057 |
| D-354 | 5 | 40 | 34 | 46.5 | 964.597 | 300 | 179.37 | 18.5 | 5.378 | 399.8288 |
| D-345 | 5 | 50 | 43.7 | 56.8 | 773.158 | 85 | 53.13 | 3.5 | 14.554 | 134.0889 |
| D-346 | 5 | 50 | 43.7 | 56.8 | 793.004 | 130 | 85.63 | 5.5 | 9.261 | 182.8485 |
| D-347 | 5 | 50 | 43.7 | 56.8 | 790.28 | 195 | 131.88 | 8.5 | 5.993 | 255.9879 |
| D-348 | 5 | 50 | 43.7 | 56.8 | 781.891 | 280 | 191.88 | 12.5 | 4.075 | 353.5072 |
| D-349 | 5 | 50 | 43.7 | 56.8 | 782.992 | 410 | 284.38 | 18.5 | 2.753 | 499.786 |
| D-340 | 5 | 63 | 56.5 | 71 | 629.924 | 120 | 86.58 | 3.5 | 7.275 | 168.952 |
| D-341 | 5 | 63 | 56.5 | 71 | 616.696 | 180 | 133.2 | 5.5 | 4.63 | 230.3891 |
| D-342 | 5 | 63 | 56.5 | 71 | 623.505 | 275 | 208.13 | 8.5 | 2.996 | 322.5448 |
| D-343 | 5 | 63 | 56.5 | 71 | 613.918 | 395 | 301.37 | 12.5 | 2.037 | 445.419 |
| D-344 | 5 | 63 | 56.5 | 71 | 621.076 | 585 | 451.22 | 18.5 | 1.376 | 629.7303 |
| D-385 | 6.3 | 32 | 24.7 | 39.6 | 1719.977 | 50 | 12.29 | 3.5 | 139.93 | 136.2429 |
| D-386 | 6.3 | 32 | 24.7 | 39.6 | 2043.089 | 75 | 22.94 | 5.5 | 89.047 | 185.7858 |
| D-387 | 6.3 | 32 | 24.7 | 39.6 | 2098.612 | 110 | 36.42 | 8.5 | 57.618 | 260.1001 |
| D-388 | 6.3 | 32 | 24.7 | 39.6 | 2065.885 | 155 | 52.73 | 12.5 | 39.18 | 359.1859 |
| D-389 | 6.3 | 32 | 24.7 | 39.6 | 2109.513 | 225 | 79.68 | 18.5 | 26.473 | 507.8145 |
| D-380 | 6.3 | 40 | 32.7 | 47.5 | 1562.682 | 60 | 21.81 | 3.5 | 71.644 | 170.3037 |
| D-381 | 6.3 | 40 | 32.7 | 47.5 | 1695.55 | 90 | 37.19 | 5.5 | 45.592 | 232.2323 |
| D-382 | 6.3 | 40 | 32.7 | 47.5 | 1777.615 | 135 | 60.26 | 8.5 | 29.501 | 325.1252 |
| D-383 | 6.3 | 40 | 32.7 | 47.5 | 1825.76 | 195 | 91.01 | 12.5 | 20.06 | 448.9824 |
| D-384 | 6.3 | 40 | 32.7 | 47.5 | 1791.169 | 280 | 132.15 | 18.5 | 13.554 | 634.7682 |
| D-375 | 6.3 | 50 | 42.6 | 57.7 | 1506.22 | 80 | 41.06 | 3.5 | 36.682 | 212.8796 |
| D-376 | 6.3 | 50 | 42.6 | 57.7 | 1424.186 | 115 | 61.01 | 5.5 | 23.343 | 290.2903 |
| D-377 | 6.3 | 50 | 42.6 | 57.7 | 1486.8 | 175 | 98.44 | 8.5 | 15.104 | 406.4065 |
| D-378 | 6.3 | 50 | 42.6 | 57.7 | 1472.179 | 250 | 143.33 | 12.5 | 10.271 | 561.228 |
| D-379 | 6.3 | 50 | 42.6 | 57.7 | 1479.452 | 365 | 213.18 | 18.5 | 6.94 | 793.4602 |
| D-370 | 6.3 | 63 | 55 | 72 | 1188.958 | 105 | 64.84 | 3.5 | 18.338 | 268.2283 |
| D-371 | 6.3 | 63 | 55 | 72 | 1156.284 | 155 | 99.09 | 5.5 | 11.669 | 365.7658 |
| D-372 | 6.3 | 63 | 55 | 72 | 1173.856 | 235 | 155.46 | 8.5 | 7.551 | 512.0721 |
| D-373 | 6.3 | 63 | 55 | 72 | 1175.608 | 340 | 228.96 | 12.5 | 5.135 | 707.1472 |
| D-374 | 6.3 | 63 | 55 | 72 | 1185.488 | 500 | 341.71 | 18.5 | 3.469 | 999.7599 |
| D-365 | 6.3 | 80 | 72 | 88.7 | 920.734 | 145 | 102.81 | 3.5 | 8.956 | 340.6073 |
| D-366 | 6.3 | 80 | 72 | 88.7 | 916.989 | 220 | 160.9 | 5.5 | 5.699 | 464.4645 |
| D-367 | 6.3 | 80 | 72 | 88.7 | 967.989 | 355 | 262.5 | 8.5 | 3.688 | 650.2503 |
| D-368 | 6.3 | 80 | 72 | 88.7 | 932.126 | 490 | 371.73 | 12.5 | 2.508 | 897.9647 |
| D-369 | 6.3 | 80 | 72 | 88.7 | 933.562 | 720 | 551 | 18.5 | 1.694 | 1269.5364 |
| D-410 | 8 | 40 | 30.8 | 49.3 | 3194.8 | 65 | 17.15 | 3.5 | 186.286 | 274.6141 |
| D-411 | 8 | 40 | 30.8 | 49.3 | 2839.164 | 90 | 23.95 | 5.5 | 118.545 | 374.4738 |
| D-412 | 8 | 40 | 30.8 | 49.3 | 3194.8 | 135 | 41.65 | 8.5 | 76.706 | 524.2633 |
| D-413 | 8 | 40 | 30.8 | 49.3 | 3142.64 | 190 | 60.25 | 12.5 | 52.16 | 723.9827 |
| D-414 | 8 | 40 | 30.8 | 49.3 | 3194.8 | 275 | 90.65 | 18.5 | 35.243 | 1023.5617 |
| D-405 | 8 | 50 | 40.8 | 59.5 | 2533.188 | 75 | 26.56 | 3.5 | 95.378 | 343.2676 |
| D-406 | 8 | 50 | 40.8 | 59.5 | 2611.224 | 110 | 43.02 | 5.5 | 60.695 | 468.0922 |
| D-407 | 8 | 50 | 40.8 | 59.5 | 2561.24 | 160 | 65.22 | 8.5 | 39.273 | 655.3291 |
| D-408 | 8 | 50 | 40.8 | 59.5 | 2620.936 | 230 | 98.14 | 12.5 | 26.706 | 904.9783 |
| D-409 | 8 | 50 | 40.8 | 59.5 | 2752.3 | 340 | 152.53 | 18.5 | 18.045 | 1279.4521 |
| D-400 | 8 | 63 | 53.6 | 73.1 | 2173.994 | 95 | 45.6 | 3.5 | 47.68 | 432.5172 |
| D-401 | 8 | 63 | 53.6 | 73.1 | 2169.66 | 140 | 71.51 | 5.5 | 30.342 | 589.7962 |
| D-402 | 8 | 63 | 53.6 | 73.1 | 2117.9 | 205 | 107.87 | 8.5 | 19.633 | 825.7147 |
| D-403 | 8 | 63 | 53.6 | 73.1 | 2198.788 | 300 | 164.7 | 12.5 | 13.35 | 1140.2727 |
| D-404 | 8 | 63 | 53.6 | 73.1 | 2186.881 | 435 | 242.43 | 18.5 | 9.021 | 1612.1097 |
| D-395 | 8 | 80 | 70 | 90.8 | 1723.143 | 125 | 74 | 3.5 | 23.286 | 549.2282 |
| D-396 | 8 | 80 | 70 | 90.8 | 1615.182 | 180 | 109 | 5.5 | 14.818 | 748.9476 |
| D-397 | 8 | 80 | 70 | 90.8 | 1764.235 | 285 | 184 | 8.5 | 9.588 | 1048.5266 |
| D-398 | 8 | 80 | 70 | 90.8 | 1753.88 | 410 | 269 | 12.5 | 6.52 | 1447.9653 |
| D-399 | 8 | 80 | 70 | 90.8 | 1757.757 | 600 | 399 | 18.5 | 4.405 | 2047.1234 |
| D-390 | 8 | 100 | 89 | 111 | 1390.586 | 170 | 116.64 | 3.5 | 11.922 | 686.5353 |
| D-391 | 8 | 100 | 89 | 111 | 1405.759 | 260 | 185.29 | 5.5 | 7.587 | 936.1845 |
| D-392 | 8 | 100 | 89 | 111 | 1390.586 | 390 | 283.26 | 8.5 | 4.909 | 1310.6583 |
| D-393 | 8 | 100 | 89 | 111 | 1403.939 | 570 | 420.56 | 12.5 | 3.338 | 1809.9567 |
| D-394 | 8 | 100 | 89 | 111 | 1401.863 | 835 | 621.51 | 18.5 | 2.256 | 2558.9042 |
| D-435 | 10 | 50 | 38 | 62 | 3536.518 | 75 | 15.19 | 3.5 | 232.857 | 536.3557 |
| D-436 | 10 | 50 | 38 | 62 | 4065.739 | 110 | 27.44 | 5.5 | 148.182 | 731.3941 |
| D-437 | 10 | 50 | 38 | 62 | 4632.316 | 165 | 48.31 | 8.5 | 95.882 | 1023.9518 |
| D-438 | 10 | 50 | 38 | 62 | 4421.375 | 230 | 67.81 | 12.5 | 65.2 | 1414.0286 |
| D-439 | 10 | 50 | 38 | 62 | 4606.402 | 335 | 104.56 | 18.5 | 44.054 | 1999.1439 |
| D-430 | 10 | 63 | 51 | 75 | 4122.691 | 96 | 35.42 | 3.5 | 116.407 | 675.8082 |
| D-431 | 10 | 63 | 51 | 75 | 3794.636 | 135 | 51.23 | 5.5 | 74.077 | 921.5566 |
| D-432 | 10 | 63 | 51 | 75 | 3903.573 | 200 | 81.44 | 8.5 | 47.932 | 1290.1792 |
| D-433 | 10 | 63 | 51 | 75 | 3913.159 | 285 | 120.06 | 12.5 | 32.594 | 1781.6761 |
| D-434 | 10 | 63 | 51 | 75 | 3864.709 | 410 | 175.49 | 18.5 | 22.023 | 2518.9214 |
| D-425 | 10 | 80 | 68 | 93 | 3021.003 | 115 | 53.14 | 3.5 | 56.85 | 858.1691 |
| D-426 | 10 | 80 | 68 | 93 | 3227.73 | 175 | 89.22 | 5.5 | 36.177 | 1170.2306 |
| D-427 | 10 | 80 | 68 | 93 | 3121.326 | 255 | 133.34 | 8.5 | 23.409 | 1638.3228 |
| D-428 | 10 | 80 | 68 | 93 | 3191.553 | 370 | 200.5 | 12.5 | 15.918 | 2262.4458 |
| D-429 | 10 | 80 | 68 | 93 | 3213.064 | 540 | 298.74 | 18.5 | 10.755 | 3198.6303 |
| D-420 | 10 | 100 | 88 | 114 | 2510.491 | 150 | 86.25 | 3.5 | 29.107 | 1072.7114 |
| D-421 | 10 | 100 | 88 | 114 | 2616.335 | 230 | 141.25 | 5.5 | 18.523 | 1462.7882 |
| D-422 | 10 | 100 | 88 | 114 | 2621.783 | 345 | 218.75 | 8.5 | 11.985 | 2047.9035 |
| D-423 | 10 | 100 | 88 | 114 | 2638.563 | 500 | 323.75 | 12.5 | 8.15 | 2828.0573 |
| D-424 | 10 | 100 | 88 | 114 | 2636.36 | 730 | 478.75 | 18.5 | 5.507 | 3998.2879 |
| D-415 | 10 | 125 | 112 | 140 | 2061.019 | 205 | 138.3 | 3.5 | 14.903 | 1340.8892 |
| D-416 | 10 | 125 | 112 | 140 | 2101.663 | 315 | 221.61 | 5.5 | 9.484 | 1828.4853 |
| D-417 | 10 | 125 | 112 | 140 | 2096.084 | 475 | 341.58 | 8.5 | 6.136 | 2559.8794 |
| D-418 | 10 | 125 | 112 | 140 | 2099.766 | 690 | 503.2 | 12.5 | 4.173 | 3535.0716 |
| D-419 | 10 | 125 | 112 | 140 | 2109.352 | 1015 | 748.14 | 18.5 | 2.819 | 4997.8598 |
Unter Kugelstrahlen versteht man eine besondere Art der Oberflächenbearbeitung. Bei dem Verfahren werden Strahlmittel in speziellen Anlagen beschleunigt und zum Aufprall auf die Oberfläche der zu bearbeitenden Werkstücke, wie zum Beispiel Metallfedern, gelenkt. Das Strahlmittel besteht aus runden oder gerundeten Körnern, denen der Vorgang seinen Namen verdankt.
In der Regel tritt die höchste Beanspruchung von Metallfedern an der Werkstoffoberfläche auf. Kleine Fehler wie Kratzer, Haarrisse, Entkohlungen oder Riefen sind da keine Seltenheit. Diese können sich jedoch negativ auf die Leistung und die Lebensdauer der Federn auswirken. Mit der Verfestigung der Randschichten wird deshalb versucht, Fehler zu minimieren und die Dauerfestigkeit der Federn zu steigern. Übliche Verfahren im Maschinenbau sind zum Beispiel Oberflächen-Festwalzen, Randschichthärtung oder Randschichtnitrieren. Weil Metallfedern eine besondere und komplizierte Geometrie aufweisen, hat sich für diese Werkstücke im Lauf der Zeit jedoch nur das Kugelstrahl-Verfahren durchgesetzt. Die Dauerfestigkeit lässt sich steigern, indem in den Randschichten des Federwerkstoffs Druckspannungen erzeugt, die dünnen Randschichten kaltverfestigt und die Oberflächen geglättet werden. Damit lassen sich Oberflächenfehler erheblich reduzieren.
Ziel des Kugelstrahlens ist es, durch Umformung und damit durch Verfestigung der Oberfläche Druckeigenspannungen aufzubauen. Mit dem Verfahren lässt sich somit die Dauerhaltbarkeit von Metallfedern deutlich verbessern. Dazu werden Stahlkugeln oder gerundetes Drahtkorn durch Pressluft oder Schleuderräder mit einer hohen Geschwindigkeit auf die Federn geschossen. Durch den Vorgang wird das Oberflächenvolumen des Werkstoffs vergrößert und eine Druckeigenspannung erzeugt. Die Folge ist eine Verdichtung des Werkstoffs und damit die Verfestigung der Oberfläche, die durch die Behandlung besonders korrosionsbeständig wird und keine Risse zulässt. Der Verdichtungsgrad ist abhängig von den Strahlenbedingungen wie der Abwurfgeschwindigkeit, Behandlungsdauer oder dem Strahlwinkel sowie Korndurchmesser, -festigkeit und -zustand des Strahlmittels. Eine wichtige Rolle für die Verdichtung spielt außerdem die Härte des Federwerkstoffs. Aufgrund des hohen Korrosionsschutzes ist das Kugelstrahlen zudem eine gute Vorbereitung für nachfolgende Behandlungen wie die Oberflächenveredelung.
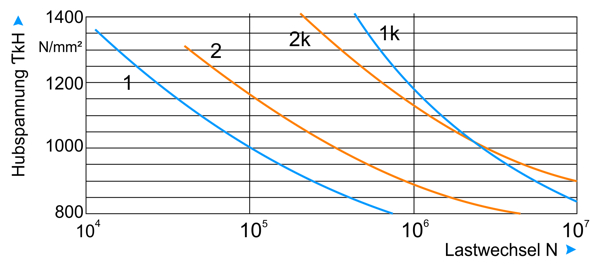
Die Abbildung zeigt ein Dauerfestigkeitsdiagramm – oder auch Wöhlerkurven genannt – für Druckfedern aus patentiert gezogenem (blaue Kurven 1) und vergütetem Ventilfederdraht (orangene Kurven 2). Die Steigerung der Zeit- und Dauerfestigkeit kugelgestrahlter (Kurve 1k und 2k) gegenüber ungestrahlter (Kurve 1 und 2) Federn ist deutlich erkennbar. Beim Kugelstrahlen entstehen umvermeidbare Spannungsspitzen in Oberflächennähe. Diese führen gegenüber ungestrahlten Federn zu einer größeren Relaxation. Sie kann durch ein Entspannen nach dem Strahlen bei einer Temperatur von 200 bis 240 °C vermieden werden. Um die Steigerung der Dauerfestigkeit langfristig zu erhalten, gilt es, werkstoffabhängige Temperaturgrenzen einzuhalten.
Zu den häufigsten Fehlern gehört das Strahlen mit scharfkantigen oder gebrochenen Körnern. Das kann zur Folge haben, dass die Dauerfestigkeit durch die Kerbwirkung unter den Wert von ungestrahlten Federn absinkt. Vermieden werden sollte zudem Überstrahlen. Bei zu langer Strahldauer oder zu hoher Abwurfgeschwindigkeit sind sowohl die Entstehung schuppenartiger Werkstofftrennungen als auch Spannungsrisse möglich. Die Behandlungsdauer der Metallfeder sollte deshalb so kurz gewählt werden, dass der Eigenspannungsaufbau die gewünschte Steigerung der Dauerfestigkeit erbringt.
Unter den Links finden Sie Informationen zu weiteren Oberflächenbehandlungen für Metallfedern. Eine Dauerfestigkeitsberechnung für eine Druckfeder mit verfestigter Oberfläche durch Kugelstrahlen können Sie mit dem Gutekunst-Federnberechnungsprogramm WinFSB durchführen.
Alternativ können Sie Ihre Federdaten auch direkt an uns schicken: verkauf@gutekunst-co.com.
Weiterführende Links:
Der Begriff Torsionsfeder leitet sich von dem Verb tordieren ab, was verwinden oder verdrehen bedeutet. Wie der Name also schon beschreibt, sind Torsionsfedern Federtypen, die während ihrem Einsatz eine permanente Drehbewegung durchführen. Sie bestehen aus Drähten, Bändern oder Stäben mit meist rundem Querschnitt, die an den beiden äußeren Seiten an Bauteilen befestigt sind. Diese führen gegeneinander eine Art Schwenkbewegung um die Achse der Feder aus – dies wird auch als Torsionsmoment bezeichnet. Torsionsfedern kommen vor allem bei Anwendungen zum Einsatz, bei denen ein Drehmoment erzeugt oder Rotationsenergie gesammelt werden soll.
Torsionsfedern sind vielseitig einsetzbar. Anwendungsgebiete sind unter anderem der Industrie- und Anlagenbau wie auch die Automobilbranche. Darüber hinaus werden Torsionsfedern aber auch beispielsweise in Sektional-Garagentoren verbaut.
Ihre vielfältigen Einsatzmöglichkeiten fordern unterschiedliche Ausführungen: Neben geraden Torsionsfedern, die als Stab- oder Drehstabfedern bezeichnet werden, gibt es auch Schraubendruckfedern und Schraubenzugfedern, die eine gewundene Form aufweisen.
Die Stab- oder Drehstabfeder hat einen gestreckten, stabförmigen Aufbau. Wird der Stab um seine eigene Längsachse verdreht, entsteht eine Schubspannung. Diese wächst mit dem Querschnittsradius (r) an und ist außerdem proportional zum Torsionsmoment (Mt). Im Stabquerschnitt verhält sich die Schubspannungsverteilung rotationssymmetrisch. Auch der Verdrehwinkel (φ) ist proportional zum Torsionsmoment und vergrößert sich linear mit der Stablänge.
Eingesetzt werden Drehstäbe beispielsweise als Torsionspendel in mechanischen Uhren, als Torsionsband in Drehspulmessinstrumenten sowie als Stabilisator zur Federung von Fahrzeugen.

Schraubenfedern bestehen aus Federstahldraht, der in Schraubenform gewunden ist. Unterschieden wird bei den Schraubfedern zwischen Schraubendruckfedern oder Schraubenzugfedern. Sie werden ihrer Bezeichnung entsprechend entweder zusammengepresst oder auseinandergezogen und umgangssprachlich als Druckfeder und Zugfeder benannt. Durch ihre verschiedenen Bauformen – zylindrisch, kegel- und tonnenförmig – werden sie vielseitig eingesetzt.
Im Gegensatz zu den geraden Stab- oder Drehstabfedern ist die Spannungsverteilung bei Schraubenfedern im Querschnitt nicht rotationssymmetrisch. Die Spannung der konkaven Randfasern ist erhöht und muss mit Korrekturfaktoren ausgeglichen werden. Wenn bei der Herstellung der Krümmung keine Wärmenachbehandlung erfolgt, wird die zulässige Spannung gemindert.
Die Federrate oder Federkonstante (c) beschreibt die Torsionsbeanspruchung. Sie kann mit der folgenden Formel berechnet werden:
Dabei gelten die nachstehenden Formelzeichen:
c = Federkonstante
F = belastende Kraft
f = Federweg
d = Drahtdurchmesser
D = mittlerer Windungsdurchmesser
i = Anzahl federnden Windungen
G = Schubmodul
Weiterführende Links:
Das Goodman-Diagramm ermöglicht die Darstellung der Dauerfestigkeit von Schraubenfedern. Zurückzuführen ist es auf das Smith-Diagramm. Dieses wird für die Berechnung der Dauerfestigkeit dynamisch beanspruchter Bauteile, bei denen die Belastung schwellend oder wechselnd ist, verwendet. Im Goodman-Diagramm wird hingegen nur die schwellende Belastung erfasst. Denn Schraubenfedern, wie Druck- oder Zugfedern, werden jeweils nur in eine Richtung beansprucht – entweder auf Zug oder auf Druck.
Als Grundlage für die Federnberechnung dient das Smith-Diagramm. Dieses wiederum richtet sich nach dem Wöhler-Verfahren, mit dem die Betriebsfestigkeit unterschiedlicher Bauteile erfasst wird.
Ermittlung der Wöhlerkurve
Mit geeigneten Probemaschinen werden Schraubenfedern so lange Schwingversuchen mit unterschiedlich hohen Spannungsausschlägen ausgesetzt, bis das Material bricht oder eine ausreichende Anzahl der Proben die Grenzschwingspielzahl ohne Bruch erreicht. Die Zeit- und Dauerfestigkeitswerte werden in einem Wöhler-Diagramm festgehalten und die Nennspannungsamplitude darin über der Schwingspielzahl dargestellt. Durch die Anwendung statischer Auswerteverfahren erhält man als Begrenzung des Streufeldes die sogenannten Wöhler-Linien. Die Überlebenswahrscheinlichkeit der Proben beträgt damit 90 Prozent.
Ableitung des Smith-Diagramms
Aus der Vielzahl von Wöhler-Linien, die für unterschiedliche Beanspruchungsverhältnisse ermittelt wurden, entsteht das Dauerfestigkeitsschaubild nach Smith. Dieses beinhaltet sowohl Wechsel- als auch Schwellfestigkeiten und dient als Grundlage für das daraus abgeleitete vereinfachte Goodman-Diagramm.
Das abgebildete Goodman-Diagramm stellt den möglichen Dauerfestigkeitsbereich des Federwerkstoffes zwischen der Oberspannung ƬkO und der Unterspannung ƬkU für eine Lastspielzahl von 107 Lastwechseln dar. Die Druckfeder ist dauerfest, wenn die berechnete Hubspannung ƬkH (Ƭk1 bis Ƭk2) innerhalb des eingegrenzten Dauerfestigkeitsbereiches bleibt.
Ragt die Hubspannung im Goodman-Diagramm jedoch über die Dauerfestigkeitsgrenze hinaus, ist die Metallfeder nicht dauerfest und muss erneut berechnet werden:
Das Goodman-Diagramm wird bei der Dauerfestigkeitsberechnung von Druckfedern im Federnberechnungsprogramm WinFSB ausgewiesen.
Weitere informative Links:
Der Begriff Dauerfestigkeit stammt aus der Werkstoffkunde. Er bezeichnet das Verformungs- sowie das Versagens-Verhalten eines schwingenden (dynamisch) belasteten Werkstoffs für eine definierte Anzahl von Zyklen. Besonders bei stark beanspruchten Druckfedern ist es wichtig, die Dauerfestigkeit zu erfassen.
Die Dauerfestigkeit wird mit Hilfe des Wöhlerversuchs berechnet, aus dessen Ergebnissen sich die sogenannte Wöhlerkurve in einem Dauerfestigkeitsschaubild skizzieren lässt. Abhängig von der Auschlagsspannung gibt sie die Zahle der Lastwechsel an, die der Werkstoff erträgt. Die Kurve in der Abbildung zeigt zudem, dass der Bruch bei Spannungen deutlich unterhalb der Zugfestigkeit Rm auftritt. Die Wöhlerkurve lässt sich in Dauerfestigkeit, Zeitfestigkeit und Kurzzeitfestigkeit aufteilen.
K gibt den Bereich der Kurzzeitschwingfestigkeit oder auch Kurzzeitfestigkeit unterhalb von etwa 104 bis 105 Schwingspielen an. Besonders bei hohen plastischen Dehnamplituden tritt diese Ermüdung häufig auf und führt zu einem vorzeitigen Versagen. Die Kurzzeitfestigkeit hat für technische Anforderungen allerdings nur eine niedrige Bedeutung.
Z kennzeichnet den Bereich der Zeitschwingfestigkeit (kurz: Zeitfestigkeit) oder auch Betriebsfestigkeit zwischen 104 und materialabhängig etwa 2·106 Schwingspielen. Die Wöhlerkurve verläuft darin bei einer doppellogarithmischen Darstellung fast gerade.
D markiert die Dauerschwingfestigkeit oder kurz Dauerfestigkeit. Bei ferritisch-perlitischen Stählen fängt diese bei etwa 1-5·106 Lastwechseln an. Ständige Korrosion sowie stark erhöhte Temperaturen, denen ein Bauteil ausgesetzt ist, führen dazu, dass die Dauerfestigkeit nicht mehr sichergestellt werden kann. Als prozentualer werkstoffabhängiger Kraftverlust muss neben der Dauerfestigkeit stark beanspruchter Druckfedern auch die Relaxation berücksichtigt werden.
Hier finden Sie Näheres zu der Relaxation bei Metallfedern , der Dauerfestigkeitsberechnung von Druckfedern (Video) und ein paar Dauerfestigkeitsschaubilder unterschiedlicher Federwerkstoffe aus dem Buch Roloff/Matek „Maschinenelemente“ (Seite 102/103).
Weitere Informationen:
Bei konischen Druckfedern verändert sich der Durchmesser der Bauform zu den Enden hin, das heißt wird größer oder kleiner. Zum Einsatz kommen sie hauptsächlich dann, wenn der Bauraum in axialer Richtung beschränkt ist. Die Besonderheit: Die Windungen bei konischen Druckfedern fallen ineinander. Damit entspricht die Blockhöhe etwa der doppelten Drahtdicke und ist dadurch wesentlich geringer als bei zylindrischen Druckfedern. Die Federn können sowohl mit linearer als auch mit progressiver Federkonstante konstruiert werden. Im Normalfall ist die Ferderrate oder Federkonstante progressiv. Das bedeutet, dass die Federkraft bei steigender Belastung zunimmt. Eine lineare Konstante wird erreicht, indem die Gewindesteigung dem Federdurchmesser entsprechend geändert wird. Dann bleibt die Federkennlinie während der Belastung konstant. Konische Federn werden nach EN 13906-1 berechnet.
Zylindrische Druckfeder: Als normale Druckfeder bezeichnet man eine Feder mit einer zylindrischen Bauform sowie einer linearen Kennlinie.
Einfache konische Druckfeder: Bei diesem Federntyp verkleinert sich der Windungsdurchmesser von Dy nach Di. Die Federkennlinie ist dabei meist progressiv ansteigend. Die Feder hat in der Regel ein offenes und ein eingerolltes Ende, das auch als Pigtail bezeichnet wird.
Doppelkonische Druckfeder: Die doppelkonische Druckfeder wird auch als Tonnenfeder bezeichnet, da beide Federenden einen kleineren Windungsdurchmesser aufweisen, als die Mitte. Sie besitzt meist eine progressive Federkennlinie.
Miniblockfeder: Der Begriff Miniblockfeder geht auf den angepassten Windungsdurchmesser zurück:
Wird die Miniblockfeder auf eine kurze Länge zusammengedrückt, passt der größte Teil der Windungen ineinander, ohne sich zu berühren. Dieser Federntyp wird häufig in der Achsfederung eines Autos eingesetzt – je nach Anforderung für eine lineare Federrate mit variablen Windungen oder für eine progressive, sich steigernde Federrate mit konstanten Windungen. Ein großer Vorteil ist die kleine und dadurch platzsparende Blocklänge der Feder. Von Nutzen ist dies zum Beispiel auf der hinteren Seite eines Fahrzeugs, bei dem eine flache Beladungsfläche gefordert wird.
Taillenfeder: Der Windungsdurchmesser der Taillenfeder oder doppelkonischen Druckfeder vergrößert sich zu den Federnenden hin. Die Federkonstante bzw. Federkennlinie ist progressiv. Zum Einsatz kommt sie beispielsweise zur Polsterung von Sesseln, Sofas und Matratzen.
Bienenkorbfeder: Die Bienenkorbfeder besitzt durch die reduzierte Masse des einseitigen eingerollten Endes sehr gute dynamische Eigenschaften.
Bei Bedarf an einer konischen Druckfeder senden Sie Ihre Anforderungen, mit Hilfe des Anfrageformulars oder einer Zeichnung, einfach an technik@gutekunst-co.com. Wir erstellen Ihnen gerne ein Angebot.
Weitere Informationen:
 Druckfedern, Zugfedern und Schenkelfedern sind typische C-Teile: Sie stehen nicht im Fokus des Beschaffungsprozesses, werden aber in nahezu allen technischen Anwendungen verbaut. Dabei sind die Anforderungen an die Federauslegung sehr vielseitig und individuell. Druck, Zug- oder Biegebelastung? Klein oder groß? Mit geformten Enden oder geradlinig? Extrem widerstandsfähig oder Standard? Lineare oder progressive Kennlinie?
Druckfedern, Zugfedern und Schenkelfedern sind typische C-Teile: Sie stehen nicht im Fokus des Beschaffungsprozesses, werden aber in nahezu allen technischen Anwendungen verbaut. Dabei sind die Anforderungen an die Federauslegung sehr vielseitig und individuell. Druck, Zug- oder Biegebelastung? Klein oder groß? Mit geformten Enden oder geradlinig? Extrem widerstandsfähig oder Standard? Lineare oder progressive Kennlinie?
Da ist es wichtig, dass der Federnanbieter flexibel auf Kundenwünsche reagieren und neben den schnell ab Lager verfügbaren Standardfedern auch individuelle Spezialfedern liefern kann. Gutekunst Federn bietet mit seinem umfangreichen Katalogprogramm mit 12.603 Federbaugrößen ab Lager und der individuellen Federnherstellung bis 12 Millimeter Drahtstärke genau diese Flexibilität. Passt eine der Katalogfedern in klassischer zylindrischer Bauform in Normalstahl EN 10270-1 und rostfrei 1.431, dann ist der Bedarf schnell gedeckt. In speziellen Anwendungsfällen wird die Feder genau auf die Einbausituation und die individuellen Anforderungen abgestimmt: als zylindrische Feder, Kegelfeder, Tonnenfeder oder Bienenkorbfeder mit variablen Federkennlinien und Windungsabständen. Dabei erfolgt die Auslegung und Berechnung der Druckfedern, Zugfedern und Schenkelfedern nach DIN EN 13906 mit verschiedenen Konstruktionshilfsmitteln und dem Erfahrungsschatz von Gutekunst Federn.
Metallfedern sind kleine Kraftspeicher, die bei Belastung Energie aufnehmen und bei Entlastung wieder abgeben. Abhängig von den Anforderungen wird jede Feder aus Federstahldraht an einem Federwindeautomat hergestellt. Die Metallfeder ist somit ein rein mechanisches Produkt. Damit kommt der Federauslegung eine hohe Bedeutung zu, denn eine nachträgliche Änderung über ein Software-Update oder eine Funktionsanpassung ist nicht möglich. Folglich erfordert die Entwicklung einer Metallfeder besondere Aufmerksamkeit und auch spezielle Konstruktionshilfsmittel wie ein Federnberechnungsprogramm, nutzenstiftende Informationen und Konstruktionsdaten in Form von CAD-Daten und Diagrammen. Und außerdem natürlich einen erfahrenen Federnhersteller, der die geforderten Eigenschaften durch das richtige Winden von Federstahldraht erreicht.
Gutekunst ist so ein erfahrener Federnhersteller, der seit 1963 Metallfedern aus Federstahldraht herstellt. Gutekunst Federn ist aber auch ein Service-Dienstleister und Entwicklungshelfer rundum die Federntechnik, der für seine Kunden und Interessenten die richtigen Servicetools zur Federnentwicklung zur Verfügung stellt.
Unter http://blog.federnshop.com steht seit 2015 ein Infoblog über das Thema Metallfedern für jedermann zur Verfügung. Egal, ob ein Techniker auf der Suche nach Materialeigenschaften ist oder ein Ingenieur Berechnungsformeln zur Federnberechnung benötigt: Der von Gutekunst Federn geführte Infoblog dreht sich komplett um das Thema Metallfedern. Neben tief gehenden Produktinformationen vermittelt der Infoblog vor allem technisches Wissen und Know-how. Ein Redaktionsteam erstellt laufend interessante Beiträge zum Thema Metallfedern. Gerne werden auch Kundenanfragen zu ganz speziellen Themen aufbereitet. Hierfür können über das Fragezeichen „?“ rechts oben im Infoblog alle Fragen zum Thema Metallfedern gestellt werden, die schon immer von Interesse waren.
300.000 Installationen weltweit und 2.500 Online-Zugriffe täglich zeigen es deutlich: Mit dem unabhängigen, kostenlosen Federnberechnungsprogramm WinFSB deckt Gutekunst Federn die Bedürfnisse vieler Konstrukteure, Studenten und Federninteressierter ab.
 WinFSB ist ein Federnberechnungsprogramm für Druckfedern, Zugfedern und Schenkelfedern, das nach der Deutschen Norm für Federn und dem Erfahrungsschatz von Gutekunst Federn entwickelt wurde. Die Berechnung kann nach unterschiedlichsten Varianten durchgeführt werden, beispielsweise ob die Metallfeder nach Weg- und Kräfteverhältnissen berechnet werden soll oder einfach nach Baumaßeigenschaften. Das Federnberechnungsprogramm berechnet die gewünschte Metallfeder mit allen wichtigen Parametern, bietet zusätzlich verschiedene Diagramme, wie beispielsweise das Goodman-Diagramm, und eine direkte Schnittstelle zum Gutekunst CAD-Generator für 2D- und 3D-CAD-Daten. Das Federnberechnungsprogramm WinFSB steht als Online-Federnberechnung und Offline-Federnberechnung (PC-Version) jedermann frei zur Verfügung.
WinFSB ist ein Federnberechnungsprogramm für Druckfedern, Zugfedern und Schenkelfedern, das nach der Deutschen Norm für Federn und dem Erfahrungsschatz von Gutekunst Federn entwickelt wurde. Die Berechnung kann nach unterschiedlichsten Varianten durchgeführt werden, beispielsweise ob die Metallfeder nach Weg- und Kräfteverhältnissen berechnet werden soll oder einfach nach Baumaßeigenschaften. Das Federnberechnungsprogramm berechnet die gewünschte Metallfeder mit allen wichtigen Parametern, bietet zusätzlich verschiedene Diagramme, wie beispielsweise das Goodman-Diagramm, und eine direkte Schnittstelle zum Gutekunst CAD-Generator für 2D- und 3D-CAD-Daten. Das Federnberechnungsprogramm WinFSB steht als Online-Federnberechnung und Offline-Federnberechnung (PC-Version) jedermann frei zur Verfügung.
Konstrukteure arbeiten heute ausschließlich mit CAD-Programmen. Das verstärkt grundsätzlich den Trend zu Standardprodukten. Hier liegen die CAD-Daten bereits vor, die Konstrukteure verlieren keine Zeit: Einfach auf der Anbieter-Website die Daten herunterladen und in das Konstruktionsprogramm einspielen. Gutekunst Federn bietet jedoch neben seinem CAD-Daten-Angebot für das Standardfedernprogramm auch direkt CAD-Daten für individuell berechnete Metallfedern an. Damit kann jeder Konstrukteur seine Wunschfeder über WinFSB berechnen und anschließend sofort im 2D- und 3D-Format herunterladen. So ist es für individuelle CAD-Daten schon ausreichend eine einfache Baumaßberechnung nach Drahtstärke „d“, äußerem Windungsdurchmesser „De“, ungespannt Länge „L0“ und Anzahl der Windungen durchzuführen, um die benötigten CAD-Daten zu erhalten. Gleich testen, hier geht’s zum Federnberechnungsprogramm WinFSB.
Das „Federn 1×1″ von Gutekunst Federn ist eine kostenlose, 24-seitige Konstruktions- und Informationsbroschüre für Druckfedern, Zugfedern und Schenkelfedern. Das „Federn 1×1“ liefert neben Berechnungsgrundlagen, form- und materialspezifischen Angaben sowie Informationen zu Bearbeitung und Betriebsverhalten auch direkte Verweise zu weiterführenden Programmen im Internet. Die leicht verständliche Broschüre richtet sich an erfahrene Konstrukteure, aber auch an Konstruktionseinsteiger. Die Informationsbroschüre kann kostenlos unter service@gutekunst-co.com als Printversion angefordert werden, oder hier als PDF-Version heruntergeladen werden.
Selbstverständlich übernimmt die Technik- und Entwicklungsabteilung von Gutekunst Federn bei Bedarf auch die komplette Entwicklung der gewünschten Metallfeder. Senden Sie einfach Ihre Anforderungen oder eine Zeichnung der gewünschten Metallfeder an die E-Mail-Adresse technik@gutekunst-co.com. Auf die Schnelle erreichen Sie die Technik- und Entwicklungsabteilung telefonisch unter (+49) 07123 960-193.
Sicherungselemente sind kleine, fast unscheinbare Maschinenkomponenten, die nahezu in jeder Konstruktion zum Einsatz kommen. Die formschlüssigen Bauteile schützen und begrenzen als Führungselemente andere Maschinenteile gegen axiales Spiel. Die Sicherungselemente sind in vielen Ausführungen erhältlich. Damit eigenen sie sich für unterschiedliche Anwendungen.
Nachfolgend eine Auswahl an Sicherungselementen von Gutekunst Federn:
Sprengringe sind Sonderformen des Sicherungsrings. Im Maschinenbau hindern sie formschlüssig Bauteile wie Räder, Dichtelemente und Lager auf Achsen, Wellen oder innerhalb von Bohrungen daran, sich axial zu verschieben. Diese Sonderformen sind vielseitig anwendbar und bieten in vielen Fällen die kostengünstigste Lösung. Sprengringe gibt es in zweierlei Ausführungen:
Gutekunst Federn bietet Sprengringe für Wellen und Bohrungen in Normalstahl EN 10270-1 und Edelstahl EN 10270-3-1.4310 ab Lager in verschiedenen Abmessungen an.
Federstecker sichern axiale Bolzen, Achsen und Verdrehsicherungen, wie etwa Kronenmuttern. Sie gehören zu den schnellen Sicherungselementen. Je nach Maß des Bolzens, der gesichert werden soll, sind die Stecker in verschiedenen Größen und zwei verschiedenen Ausführungen erhältlich:
Hier geht es zur Artikelauswahl von Federsteckern einfach und Federsteckern doppelt in Normalstahl EN 10270-1 und Edelstahl EN 10270-3-1.4310
Die Fokkernadel, auch als Sicherungsklammer bezeichnet, sichert Schraubverbindungen. Sie kommt vor allem in der Luftfahrt, aber auch in vielen weiteren Anwendungen zum Einsatz. Sie verhindert das ungewollte Lösen von Schrauben, das unter anderem durch Vibrationen verursacht werden kann. Dazu wird die Fokkernadel durch die Krone und das Gewindeloch geführt.
Hier geht es zur Artikelauswahl Fokkernadeln / Sicherungsklammern in Normalstahl EN 10270-1 und Edelstahl EN 10270-3-1.4310
Die folgenden Produkte gehören ebenfalls zu den Sicherungselementen:
Der Elastizitätsmodul ist ein Materialkennwert aus der Werkstofftechnik. Dieser Kennwert beschreibt den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers in einem linear-elastischem Verhalten. Der Elastizitätsmodul ist unter den Abkürzungen E-Modul oder als Formelzeichen E in der Federnberechnung bekannt; er hat die Einheit „N/mm²“ einer mechanischen Spannung.
Je mehr Widerstand ein Material seiner elastischen Verformung entgegensetzt, umso größer ist der Betrag des Elastizitätsmoduls. Ein Bauteil aus einem Material mit hohem Elastizitätsmodul (beispielsweise Federstahl) ist somit steifer als ein Bauteil gleicher Konstruktion (mit identischen geometrischen Abmessungen), das aus einem Material mit niedrigem Elastizitätsmodul (beispielsweise Gummi) besteht. Dabei ist der Elastizitätsmodul die Proportionalitätskonstante im Hookeschen Gesetz.
Rm = Zugfestigkeit
σ = Spannung
AL = Lüdersdehnung
Ag = Gleichmaßdehnung
A = Bruchdehnung
At = gesamte Dehnung bei Bruch
Ɛ = Dehnung
Die Definition des Elastizitätsmoduls: Der Elastizitätsmodul ist die Steigung des Graphen im Spannungs-Dehnungs-Diagramm bei einachsiger Belastung innerhalb des linearen Elastizitätsbereichs. Dieser lineare Bereich heißt auch Hookesche Gerade.
Dabei bezeichnet
σ = F/A (=Kraft/Fläche) die mechanische Spannung (Normalspannung, nicht Schubspannung) und Ɛ = ∆L/L0 die Dehnung. Die Dehnung ist das Verhältnis von Längenänderung ∆L = L – L0 zur ursprünglichen Länge L0
E – Elastizitätsmodul
σ – Spannung
ε – Dehnung
Hier gibt es das Elastizitätsmodul zur Federnberechnung bei Raumtemperatur (20°C) für die wichtigsten Federwerkstoffe.
Der Elastizitätsmodul ist aber nicht bezüglich aller physikalischen Größen konstant. So beeinflussen zudem die unterschiedlichen Umgebungseinflüsse, wie zum Beispiel Temperatur oder Feuchte, den E-Modul. Die Anpassung des Elastizitätsmoduls wird bei höheren Temperaturen nach folgender Formel ermittelt, wobei die Federwerkstoffkennwerte bei Raumtemperatur (20°C) als Basis dienen.
Weitere Informationen:
Die Norm DIN 2098 beinhaltet eine Auswahl an kaltgeformten zylindrischen Druckfedern ab 0,1 bis 10 mm Drahtstärke in 525 standardisierten Druckfederabmessungen. Die Druckfedern sind in Gütegrad 2 nach DIN EN 15800 aus normalen Federstahldraht EN 10207-1DH (bis 1,8 mm Drahtstärke) und -1SH (ab 1,8 mm Drahtstärke) gefertigt. Sie sind rechtsgewickelt (im Uhrzeigersinn) mit gleichmäßiger Steigung. Bis Drahtdurchmesser 0,45 mm sind die Endwindungen „angelegt“, größere Drahtstärken haben „angelegte und geschliffene“ Endwingungen. Die Druckfedern sind angelassen und werden je nach Setzverhalten, vorgesetzt.
Heute hat die Norm DIN 2098, die früher für eine schnelle Druckfedernauswahl und Belieferung in kleinen Stückzahlen sorgen sollte, seine Wertigkeit verloren. Viele Federnhersteller haben längst ihr Artikelangebot auf Basis der Norm DIN 2098 erweitert. So auch Gutekunst Federn, die heute in ihrem Federnkatalog ein Standardsortiment mit 12.603 Abmessungen ab Lager anbietet. Nachfolgend zusammengefasst die Druckfederabmessungen nach DIN 2098 Blatt 1 und 2.

d Drahtdurchmesser (mm)
D Mittlerer Windungsdurchmesser (mm)
Dd Größter Dorndurchmesser (mm)
Fn Höchstkraft bei statischer Belastung (N)
L0 Ungespannte Länge der Feder (mm)
sn Größter Federweg bei statischer Belastung (mm)
n Anzahl der federnden Windungen (St.)
R Federrate (N/mm)
Gew Gewicht pro Stück (g)
| Artikelnummer | d (mm) | D (mm) | Dd (mm) | Dh (mm) | Fn (N) | L0 (mm) | sn (mm) | n (St) | R (N/mm) | Gew (g) |
|---|---|---|---|---|---|---|---|---|---|---|
| D-2020 | 0.1 | 0.5 | 0.3 | 0.8 | 0.582 | 1 | 0.25 | 3.5 | 2.329 | 0.0005 |
| D-2021 | 0.1 | 0.5 | 0.3 | 0.8 | 0.629 | 1.4 | 0.42 | 5.5 | 1.482 | 0.0007 |
| D-2022 | 0.1 | 0.5 | 0.3 | 0.8 | 0.655 | 2 | 0.68 | 8.5 | 0.959 | 0.001 |
| D-2023 | 0.1 | 0.5 | 0.3 | 0.8 | 0.605 | 2.7 | 0.93 | 12.5 | 0.652 | 0.0014 |
| D-2024 | 0.1 | 0.5 | 0.3 | 0.8 | 0.637 | 3.9 | 1.45 | 18.5 | 0.441 | 0.002 |
| D-2015 | 0.1 | 0.63 | 0.4 | 0.9 | 0.517 | 1.2 | 0.44 | 3.5 | 1.164 | 0.0007 |
| D-2016 | 0.1 | 0.63 | 0.4 | 0.9 | 0.528 | 1.7 | 0.71 | 5.5 | 0.741 | 0.0009 |
| D-2017 | 0.1 | 0.63 | 0.4 | 0.9 | 0.51 | 2.4 | 1.06 | 8.5 | 0.479 | 0.0013 |
| D-2018 | 0.1 | 0.63 | 0.4 | 0.9 | 0.522 | 3.4 | 1.6 | 12.5 | 0.326 | 0.0018 |
| D-2019 | 0.1 | 0.63 | 0.4 | 0.9 | 0.53 | 4.9 | 2.4 | 18.5 | 0.22 | 0.0025 |
| D-2010 | 0.1 | 0.8 | 0.5 | 1.1 | 0.416 | 1.5 | 0.73 | 3.5 | 0.568 | 0.0009 |
| D-2011 | 0.1 | 0.8 | 0.5 | 1.1 | 0.431 | 2.2 | 1.19 | 5.5 | 0.362 | 0.0012 |
| D-2012 | 0.1 | 0.8 | 0.5 | 1.1 | 0.429 | 3.2 | 1.83 | 8.5 | 0.234 | 0.0016 |
| D-2013 | 0.1 | 0.8 | 0.5 | 1.1 | 0.439 | 4.6 | 2.76 | 12.5 | 0.159 | 0.0023 |
| D-2014 | 0.1 | 0.8 | 0.5 | 1.1 | 0.434 | 6.6 | 4.04 | 18.5 | 0.108 | 0.0032 |
| D-2005 | 0.1 | 1 | 0.7 | 1.4 | 0.353 | 2 | 1.21 | 3.5 | 0.291 | 0.0011 |
| D-2006 | 0.1 | 1 | 0.7 | 1.4 | 0.345 | 2.9 | 1.86 | 5.5 | 0.185 | 0.0015 |
| D-2007 | 0.1 | 1 | 0.7 | 1.4 | 0.358 | 4.4 | 2.99 | 8.5 | 0.12 | 0.002 |
| D-2008 | 0.1 | 1 | 0.7 | 1.4 | 0.358 | 6.3 | 4.39 | 12.5 | 0.082 | 0.0028 |
| D-2009 | 0.1 | 1 | 0.7 | 1.4 | 0.36 | 9.2 | 6.54 | 18.5 | 0.055 | 0.004 |
| D-2000 | 0.1 | 1.2 | 0.8 | 1.5 | 0.301 | 2.6 | 1.79 | 3.5 | 0.168 | 0.0013 |
| D-2001 | 0.1 | 1.2 | 0.8 | 1.5 | 0.292 | 3.8 | 2.73 | 5.5 | 0.107 | 0.0018 |
| D-2002 | 0.1 | 1.2 | 0.8 | 1.5 | 0.3 | 5.8 | 4.33 | 8.5 | 0.069 | 0.0025 |
| D-2003 | 0.1 | 1.2 | 0.8 | 1.5 | 0.302 | 8.4 | 6.41 | 12.5 | 0.047 | 0.0034 |
| D-2004 | 0.1 | 1.2 | 0.8 | 1.5 | 0.306 | 12.4 | 9.62 | 18.5 | 0.032 | 0.0048 |
| D-2046 | 0.12 | 0.63 | 0.4 | 0.9 | 1.479 | 1.2 | 0.44 | 2.5 | 3.379 | 0.0008 |
| D-2047 | 0.12 | 0.63 | 0.4 | 0.9 | 0.809 | 1.7 | 0.53 | 5.5 | 1.536 | 0.0013 |
| D-2048 | 0.12 | 0.63 | 0.4 | 0.9 | 0.811 | 2.4 | 0.82 | 8.5 | 0.994 | 0.0019 |
| D-2049 | 0.12 | 0.63 | 0.4 | 0.9 | 0.857 | 3.4 | 1.27 | 12.5 | 0.676 | 0.0026 |
| D-2050 | 0.12 | 0.63 | 0.4 | 0.9 | 0.889 | 4.9 | 1.95 | 18.5 | 0.457 | 0.0036 |
| D-2041 | 0.12 | 0.8 | 0.5 | 1.2 | 0.696 | 1.5 | 0.59 | 3.5 | 1.179 | 0.0012 |
| D-2042 | 0.12 | 0.8 | 0.5 | 1.2 | 0.683 | 2.1 | 0.91 | 5.5 | 0.75 | 0.0017 |
| D-2043 | 0.12 | 0.8 | 0.5 | 1.2 | 0.723 | 3.1 | 1.49 | 8.5 | 0.485 | 0.0024 |
| D-2044 | 0.12 | 0.8 | 0.5 | 1.2 | 0.736 | 4.4 | 2.23 | 12.5 | 0.33 | 0.0033 |
| D-2045 | 0.12 | 0.8 | 0.5 | 1.2 | 0.734 | 6.3 | 3.29 | 18.5 | 0.223 | 0.0046 |
| D-2036 | 0.12 | 1 | 0.6 | 1.4 | 0.588 | 1.9 | 0.97 | 3.5 | 0.604 | 0.0015 |
| D-2037 | 0.12 | 1 | 0.6 | 1.4 | 0.57 | 2.7 | 1.49 | 5.5 | 0.384 | 0.0021 |
| D-2038 | 0.12 | 1 | 0.6 | 1.4 | 0.584 | 4 | 2.35 | 8.5 | 0.249 | 0.0029 |
| D-2039 | 0.12 | 1 | 0.6 | 1.4 | 0.604 | 5.8 | 3.57 | 12.5 | 0.169 | 0.0041 |
| D-2040 | 0.12 | 1 | 0.6 | 1.4 | 0.606 | 8.4 | 5.31 | 18.5 | 0.114 | 0.0058 |
| D-2030 | 0.12 | 1.2 | 0.8 | 1.6 | 0.508 | 2.4 | 1.46 | 3.5 | 0.349 | 0.0019 |
| D-2031 | 0.12 | 1.2 | 0.8 | 1.6 | 0.501 | 3.5 | 2.26 | 5.5 | 0.222 | 0.0025 |
| D-2032 | 0.12 | 1.2 | 0.8 | 1.6 | 0.504 | 5.2 | 3.51 | 8.5 | 0.144 | 0.0035 |
| D-2033 | 0.12 | 1.2 | 0.8 | 1.6 | 0.509 | 7.5 | 5.21 | 12.5 | 0.098 | 0.0049 |
| D-2034 | 0.12 | 1.2 | 0.8 | 1.6 | 0.509 | 10.9 | 7.71 | 18.5 | 0.066 | 0.0069 |
| D-2025 | 0.12 | 1.6 | 1.2 | 2.1 | 0.384 | 3.6 | 2.61 | 3.5 | 0.147 | 0.0025 |
| D-2026 | 0.12 | 1.6 | 1.2 | 2.1 | 0.382 | 5.4 | 4.08 | 5.5 | 0.094 | 0.0034 |
| D-2027 | 0.12 | 1.6 | 1.2 | 2.1 | 0.387 | 8.2 | 6.39 | 8.5 | 0.061 | 0.0047 |
| D-2028 | 0.12 | 1.6 | 1.2 | 2.1 | 0.385 | 11.8 | 9.33 | 12.5 | 0.041 | 0.0065 |
| D-2029 | 0.12 | 1.6 | 1.2 | 2.1 | 0.389 | 17.4 | 13.95 | 18.5 | 0.028 | 0.0092 |
| D-2071 | 0.16 | 0.8 | 0.4 | 1.2 | 1.501 | 1.6 | 0.4 | 3.5 | 3.726 | 0.0022 |
| D-2072 | 0.16 | 0.8 | 0.4 | 1.2 | 1.515 | 2.2 | 0.64 | 5.5 | 2.371 | 0.003 |
| D-2073 | 0.16 | 0.8 | 0.4 | 1.2 | 1.523 | 3.1 | 0.99 | 8.5 | 1.534 | 0.0042 |
| D-2074 | 0.16 | 0.8 | 0.4 | 1.2 | 1.633 | 4.4 | 1.57 | 12.5 | 1.043 | 0.0058 |
| D-2075 | 0.16 | 0.8 | 0.4 | 1.2 | 1.602 | 6.2 | 2.27 | 18.5 | 0.705 | 0.0082 |
| D-2066 | 0.16 | 1 | 0.6 | 1.3 | 1.318 | 1.9 | 0.69 | 3.5 | 1.908 | 0.0027 |
| D-2067 | 0.16 | 1 | 0.6 | 1.3 | 1.36 | 2.7 | 1.12 | 5.5 | 1.214 | 0.0037 |
| D-2068 | 0.16 | 1 | 0.6 | 1.3 | 1.307 | 3.8 | 1.66 | 8.5 | 0.785 | 0.0052 |
| D-2069 | 0.16 | 1 | 0.6 | 1.3 | 1.347 | 5.4 | 2.52 | 12.5 | 0.534 | 0.0072 |
| D-2070 | 0.16 | 1 | 0.6 | 1.3 | 1.375 | 7.8 | 3.81 | 18.5 | 0.361 | 0.0102 |
| D-2061 | 0.16 | 1.2 | 0.8 | 1.6 | 1.078 | 2.2 | 0.98 | 3.5 | 1.104 | 0.0033 |
| D-2062 | 0.16 | 1.2 | 0.8 | 1.6 | 1.122 | 3.2 | 1.6 | 5.5 | 0.702 | 0.0045 |
| D-2063 | 0.16 | 1.2 | 0.8 | 1.6 | 1.15 | 4.7 | 2.53 | 8.5 | 0.455 | 0.0063 |
| D-2064 | 0.16 | 1.2 | 0.8 | 1.6 | 1.166 | 6.7 | 3.77 | 12.5 | 0.309 | 0.0087 |
| D-2065 | 0.16 | 1.2 | 0.8 | 1.6 | 1.177 | 9.7 | 5.63 | 18.5 | 0.209 | 0.0123 |
| D-2056 | 0.16 | 1.6 | 1.1 | 2.1 | 0.857 | 3.1 | 1.84 | 3.5 | 0.466 | 0.0044 |
| D-2057 | 0.16 | 1.6 | 1.1 | 2.1 | 0.901 | 4.7 | 3.04 | 5.5 | 0.296 | 0.006 |
| D-2058 | 0.16 | 1.6 | 1.1 | 2.1 | 0.909 | 7 | 4.74 | 8.5 | 0.192 | 0.0084 |
| D-2059 | 0.16 | 1.6 | 1.1 | 2.1 | 0.905 | 10 | 6.94 | 12.5 | 0.13 | 0.0116 |
| D-2060 | 0.16 | 1.6 | 1.1 | 2.1 | 0.911 | 14.6 | 10.34 | 18.5 | 0.088 | 0.0164 |
| D-2051 | 0.16 | 2 | 1.5 | 2.5 | 0.714 | 4.3 | 2.99 | 3.5 | 0.238 | 0.0055 |
| D-2052 | 0.16 | 2 | 1.5 | 2.5 | 0.723 | 6.5 | 4.77 | 5.5 | 0.152 | 0.0075 |
| D-2053 | 0.16 | 2 | 1.5 | 2.5 | 0.729 | 9.8 | 7.43 | 8.5 | 0.098 | 0.0105 |
| D-2054 | 0.16 | 2 | 1.5 | 2.5 | 0.732 | 14.2 | 10.97 | 12.5 | 0.067 | 0.0145 |
| D-2055 | 0.16 | 2 | 1.5 | 2.5 | 0.739 | 20.9 | 16.39 | 18.5 | 0.045 | 0.0205 |
| D-011R | 0.2 | 1 | 0.6 | 1.4 | 2.346 | 2 | 0.5 | 3.5 | 4.657 | 0.0043 |
| D-011S | 0.2 | 1 | 0.6 | 1.4 | 2.219 | 2.7 | 0.75 | 5.5 | 2.964 | 0.0059 |
| D-011T | 0.2 | 1 | 0.6 | 1.4 | 2.428 | 3.9 | 1.27 | 8.5 | 1.918 | 0.0082 |
| D-011U | 0.2 | 1 | 0.6 | 1.4 | 2.551 | 5.5 | 1.96 | 12.5 | 1.304 | 0.0113 |
| D-011V | 0.2 | 1 | 0.6 | 1.4 | 2.547 | 7.8 | 2.89 | 18.5 | 0.881 | 0.016 |
| D-011M | 0.2 | 1.2 | 0.8 | 1.7 | 2.135 | 2.3 | 0.79 | 3.5 | 2.695 | 0.0051 |
| D-011N | 0.2 | 1.2 | 0.8 | 1.7 | 2.111 | 3.2 | 1.23 | 5.5 | 1.715 | 0.007 |
| D-011O | 0.2 | 1.2 | 0.8 | 1.7 | 2.151 | 4.6 | 1.94 | 8.5 | 1.11 | 0.0098 |
| D-011P | 0.2 | 1.2 | 0.8 | 1.7 | 2.2 | 6.5 | 2.92 | 12.5 | 0.755 | 0.0136 |
| D-011Q | 0.2 | 1.2 | 0.8 | 1.7 | 2.208 | 9.3 | 4.33 | 18.5 | 0.51 | 0.0192 |
| D-011G | 0.2 | 1.6 | 1.1 | 2.1 | 1.777 | 3.1 | 1.56 | 3.5 | 1.137 | 0.0069 |
| D-011H | 0.2 | 1.6 | 1.1 | 2.1 | 1.725 | 4.4 | 2.38 | 5.5 | 0.724 | 0.0094 |
| D-011J | 0.2 | 1.6 | 1.1 | 2.1 | 1.717 | 6.4 | 3.67 | 8.5 | 0.468 | 0.0131 |
| D-011K | 0.2 | 1.6 | 1.1 | 2.1 | 1.754 | 9.2 | 5.51 | 12.5 | 0.318 | 0.0181 |
| D-011L | 0.2 | 1.6 | 1.1 | 2.1 | 1.758 | 13.3 | 8.17 | 18.5 | 0.215 | 0.0256 |
| D-007A | 0.2 | 2 | 1.5 | 2.6 | 0.713 | 4 | 1.93 | 5.5 | 0.37 | 0.0117 |
| D-008A | 0.2 | 2 | 1.5 | 2.6 | 1.417 | 5.9 | 3.83 | 5.5 | 0.37 | 0.0117 |
| D-009A | 0.2 | 2 | 1.5 | 2.6 | 1.408 | 8.7 | 5.88 | 8.5 | 0.24 | 0.0164 |
| D-010A | 0.2 | 2 | 1.5 | 2.6 | 1.43 | 12.6 | 8.78 | 12.5 | 0.163 | 0.0226 |
| D-011A | 0.2 | 2 | 1.5 | 2.6 | 1.429 | 18.3 | 12.98 | 18.5 | 0.11 | 0.032 |
| D-002 | 0.2 | 2.5 | 2 | 3.1 | 1.122 | 5.4 | 3.77 | 3.5 | 0.298 | 0.0107 |
| D-003 | 0.2 | 2.5 | 2 | 3.1 | 1.144 | 8.2 | 6.03 | 5.5 | 0.19 | 0.0146 |
| D-004 | 0.2 | 2.5 | 2 | 3.1 | 1.194 | 12.7 | 9.73 | 8.5 | 0.123 | 0.0205 |
| D-005 | 0.2 | 2.5 | 2 | 3.1 | 1.232 | 18.8 | 14.76 | 12.5 | 0.083 | 0.0283 |
| D-006 | 0.2 | 2.5 | 2 | 3.1 | 1.109 | 25.3 | 19.66 | 18.5 | 0.056 | 0.04 |
| D-026M | 0.25 | 1.2 | 0.7 | 1.8 | 3.502 | 2.4 | 0.53 | 3.5 | 6.58 | 0.008 |
| D-026N | 0.25 | 1.2 | 0.7 | 1.8 | 3.622 | 3.3 | 0.86 | 5.5 | 4.187 | 0.011 |
| D-026O | 0.25 | 1.2 | 0.7 | 1.8 | 3.831 | 4.7 | 1.41 | 8.5 | 2.709 | 0.0154 |
| D-026P | 0.25 | 1.2 | 0.7 | 1.8 | 4.015 | 6.6 | 2.18 | 12.5 | 1.842 | 0.0212 |
| D-026Q | 0.25 | 1.2 | 0.7 | 1.8 | 4.08 | 9.4 | 3.28 | 18.5 | 1.245 | 0.03 |
| D-026G | 0.25 | 1.6 | 1 | 2.2 | 3.078 | 3 | 1.11 | 3.5 | 2.776 | 0.0107 |
| D-026H | 0.25 | 1.6 | 1 | 2.2 | 3.229 | 4.3 | 1.83 | 5.5 | 1.766 | 0.0146 |
| D-026J | 0.25 | 1.6 | 1 | 2.2 | 3.266 | 6.2 | 2.86 | 8.5 | 1.143 | 0.0205 |
| D-026K | 0.25 | 1.6 | 1 | 2.2 | 3.261 | 8.7 | 4.2 | 12.5 | 0.777 | 0.0283 |
| D-026L | 0.25 | 1.6 | 1 | 2.2 | 3.284 | 12.5 | 6.25 | 18.5 | 0.525 | 0.04 |
| D-022A | 0.25 | 2 | 1.5 | 2.6 | 2.528 | 3.7 | 1.78 | 3.5 | 1.421 | 0.0134 |
| D-023A | 0.25 | 2 | 1.5 | 2.6 | 2.696 | 5.5 | 2.98 | 5.5 | 0.904 | 0.0183 |
| D-024A | 0.25 | 2 | 1.5 | 2.6 | 2.682 | 8 | 4.58 | 8.5 | 0.585 | 0.0256 |
| D-025A | 0.25 | 2 | 1.5 | 2.6 | 2.701 | 11.4 | 6.79 | 12.5 | 0.398 | 0.0354 |
| D-026A | 0.25 | 2 | 1.5 | 2.6 | 2.741 | 16.6 | 10.19 | 18.5 | 0.269 | 0.05 |
| D-017A | 0.25 | 2.5 | 1.9 | 3.1 | 2.133 | 4.9 | 2.93 | 3.5 | 0.728 | 0.0168 |
| D-018 | 0.25 | 2.5 | 1.9 | 3.1 | 2.179 | 7.3 | 4.71 | 5.5 | 0.463 | 0.0229 |
| D-019 | 0.25 | 2.5 | 1.9 | 3.1 | 2.208 | 10.9 | 7.37 | 8.5 | 0.3 | 0.032 |
| D-020A | 0.25 | 2.5 | 1.9 | 3.1 | 2.225 | 15.7 | 10.92 | 12.5 | 0.204 | 0.0442 |
| D-021A | 0.25 | 2.5 | 1.9 | 3.1 | 2.236 | 22.9 | 16.24 | 18.5 | 0.138 | 0.0625 |
| D-012A | 0.25 | 3.2 | 2.5 | 4 | 1.751 | 7.1 | 5.05 | 3.5 | 0.347 | 0.0215 |
| D-013A | 0.25 | 3.2 | 2.5 | 4 | 1.761 | 10.7 | 7.97 | 5.5 | 0.221 | 0.0293 |
| D-013B | 0.25 | 3.2 | 2.5 | 4 | 1.767 | 16.1 | 12.37 | 8.5 | 0.143 | 0.041 |
| D-015A | 0.25 | 3.2 | 2.5 | 4 | 1.77 | 23.3 | 18.22 | 12.5 | 0.097 | 0.0566 |
| D-016A | 0.25 | 3.2 | 2.5 | 4 | 1.772 | 34.1 | 27 | 18.5 | 0.066 | 0.08 |
| D-042F-01 | 0.32 | 1.6 | 1 | 2.2 | 5.261 | 3.1 | 0.71 | 3.5 | 7.451 | 0.0176 |
| D-042F-02 | 0.32 | 1.6 | 1 | 2.2 | 6.06 | 4.4 | 1.28 | 5.5 | 4.742 | 0.024 |
| D-042F-03 | 0.32 | 1.6 | 1 | 2.2 | 6.4 | 6.3 | 2.09 | 8.5 | 3.068 | 0.0336 |
| D-042F-04 | 0.32 | 1.6 | 1 | 2.2 | 6.322 | 8.7 | 3.03 | 12.5 | 2.086 | 0.0463 |
| D-042F-05 | 0.32 | 1.6 | 1 | 2.2 | 6.606 | 12.54 | 4.69 | 18.5 | 1.41 | 0.0655 |
| D-042B | 0.32 | 2 | 1.4 | 2.6 | 4.892 | 3.7 | 1.28 | 3.5 | 3.815 | 0.022 |
| D-042C | 0.32 | 2 | 1.4 | 2.6 | 5.198 | 5.3 | 2.14 | 5.5 | 2.428 | 0.03 |
| D-042D | 0.32 | 2 | 1.4 | 2.6 | 5.386 | 7.7 | 3.43 | 8.5 | 1.571 | 0.0419 |
| D-042E | 0.32 | 2 | 1.4 | 2.6 | 5.497 | 10.9 | 5.15 | 12.5 | 1.068 | 0.0579 |
| D-042F | 0.32 | 2 | 1.4 | 2.6 | 5.501 | 15.6 | 7.62 | 18.5 | 0.722 | 0.0819 |
| D-038A | 0.32 | 2.5 | 1.9 | 3.1 | 4.386 | 4.7 | 2.25 | 3.5 | 1.953 | 0.0275 |
| D-039A | 0.32 | 2.5 | 1.9 | 3.1 | 4.454 | 6.8 | 3.58 | 5.5 | 1.243 | 0.0374 |
| D-040A | 0.32 | 2.5 | 1.9 | 3.1 | 4.536 | 10 | 5.64 | 8.5 | 0.804 | 0.0524 |
| D-041A | 0.32 | 2.5 | 1.9 | 3.1 | 4.547 | 14.2 | 8.31 | 12.5 | 0.547 | 0.0724 |
| D-042A | 0.32 | 2.5 | 1.9 | 3.1 | 4.592 | 20.6 | 12.43 | 18.5 | 0.37 | 0.1024 |
| D-033A | 0.32 | 3.2 | 2.4 | 4 | 3.521 | 6.3 | 3.78 | 3.5 | 0.931 | 0.0352 |
| D-034A | 0.32 | 3.2 | 2.4 | 4 | 3.604 | 9.4 | 6.08 | 5.5 | 0.593 | 0.0479 |
| D-035A | 0.32 | 3.2 | 2.4 | 4 | 3.636 | 14 | 9.48 | 8.5 | 0.384 | 0.0671 |
| D-036A | 0.32 | 3.2 | 2.4 | 4 | 3.646 | 20.1 | 13.98 | 12.5 | 0.261 | 0.0927 |
| D-037A | 0.32 | 3.2 | 2.4 | 4 | 3.662 | 29.3 | 20.78 | 18.5 | 0.176 | 0.131 |
| D-028A | 0.32 | 4 | 3.2 | 4.8 | 2.902 | 8.7 | 6.09 | 3.5 | 0.477 | 0.0439 |
| D-029A | 0.32 | 4 | 3.2 | 4.8 | 2.923 | 13.1 | 9.63 | 5.5 | 0.303 | 0.0599 |
| D-030A | 0.32 | 4 | 3.2 | 4.8 | 1.782 | 19.8 | 13.34 | 12.5 | 0.134 | 0.1158 |
| D-030B | 0.32 | 4 | 3.2 | 4.8 | 2.957 | 28.6 | 22.14 | 12.5 | 0.134 | 0.1158 |
| D-032A | 0.32 | 4 | 3.2 | 4.8 | 2.967 | 41.9 | 32.88 | 18.5 | 0.09 | 0.1638 |
| D-063C | 0.4 | 2 | 1.3 | 2.7 | 8.453 | 3.9 | 0.91 | 3.5 | 9.314 | 0.0343 |
| D-063D | 0.4 | 2 | 1.3 | 2.7 | 9.469 | 5.5 | 1.6 | 5.5 | 5.927 | 0.0468 |
| D-063E | 0.4 | 2 | 1.3 | 2.7 | 9.713 | 7.8 | 2.53 | 8.5 | 3.835 | 0.0655 |
| D-063F | 0.4 | 2 | 1.3 | 2.7 | 9.943 | 10.9 | 3.81 | 12.5 | 2.608 | 0.0905 |
| D-063G | 0.4 | 2 | 1.3 | 2.7 | 10.19 | 15.6 | 5.78 | 18.5 | 1.762 | 0.1279 |
| D-059A | 0.4 | 2.5 | 1.8 | 3.2 | 8.002 | 4.7 | 1.68 | 3.5 | 4.769 | 0.0429 |
| D-060A | 0.4 | 2.5 | 1.8 | 3.2 | 8.349 | 6.7 | 2.75 | 5.5 | 3.035 | 0.0585 |
| D-061A | 0.4 | 2.5 | 1.8 | 3.2 | 8.367 | 9.6 | 4.26 | 8.5 | 1.964 | 0.0819 |
| D-062B | 0.4 | 2.5 | 1.8 | 3.2 | 8.555 | 13.6 | 6.41 | 12.5 | 1.335 | 0.1131 |
| D-063B | 0.4 | 2.5 | 1.8 | 3.2 | 8.595 | 19.5 | 9.53 | 18.5 | 0.902 | 0.1599 |
| D-053A | 0.4 | 3.2 | 2.5 | 4 | 6.653 | 6 | 2.93 | 3.5 | 2.274 | 0.0549 |
| D-054A | 0.4 | 3.2 | 2.5 | 4 | 6.756 | 8.7 | 4.67 | 5.5 | 1.447 | 0.0749 |
| D-055A | 0.4 | 3.2 | 2.5 | 4 | 6.867 | 12.8 | 7.33 | 8.5 | 0.936 | 0.1049 |
| D-056B | 0.4 | 3.2 | 2.5 | 4 | 6.953 | 18.3 | 10.92 | 12.5 | 0.637 | 0.1448 |
| D-057B | 0.4 | 3.2 | 2.5 | 4 | 6.991 | 26.5 | 16.25 | 18.5 | 0.43 | 0.2047 |
| D-048A | 0.4 | 4 | 3.2 | 4.9 | 5.53 | 7.9 | 4.75 | 3.5 | 1.164 | 0.0687 |
| D-049A | 0.4 | 4 | 3.2 | 4.9 | 5.594 | 11.7 | 7.55 | 5.5 | 0.741 | 0.0936 |
| D-050A | 0.4 | 4 | 3.2 | 4.9 | 5.681 | 17.5 | 11.85 | 8.5 | 0.479 | 0.1311 |
| D-051B | 0.4 | 4 | 3.2 | 4.9 | 5.689 | 25.1 | 17.45 | 12.5 | 0.326 | 0.181 |
| D-052B | 0.4 | 4 | 3.2 | 4.9 | 5.716 | 36.6 | 25.95 | 18.5 | 0.22 | 0.2559 |
| D-043A | 0.4 | 5 | 4.1 | 6 | 4.549 | 10.9 | 7.63 | 3.5 | 0.596 | 0.0858 |
| D-044A | 0.4 | 5 | 4.1 | 6 | 4.577 | 16.4 | 12.06 | 5.5 | 0.379 | 0.117 |
| D-045A | 0.4 | 5 | 4.1 | 6 | 4.606 | 24.7 | 18.76 | 8.5 | 0.245 | 0.1638 |
| D-046B | 0.4 | 5 | 4.1 | 6 | 4.628 | 35.8 | 27.73 | 12.5 | 0.167 | 0.2262 |
| D-047B | 0.4 | 5 | 4.1 | 6 | 4.638 | 52.4 | 41.13 | 18.5 | 0.113 | 0.3199 |
| D-086 | 0.5 | 2.5 | 1.7 | 3.3 | 16.409 | 4.4 | 1.41 | 3.5 | 11.643 | 0.067 |
| D-087 | 0.5 | 2.5 | 1.7 | 3.3 | 14.61 | 6.1 | 1.97 | 5.5 | 7.409 | 0.0914 |
| D-088 | 0.5 | 2.5 | 1.7 | 3.3 | 13.738 | 8.7 | 2.87 | 8.5 | 4.794 | 0.128 |
| D-089 | 0.5 | 2.5 | 1.7 | 3.3 | 12.683 | 12 | 3.89 | 12.5 | 3.26 | 0.1768 |
| D-090 | 0.5 | 2.5 | 1.7 | 3.3 | 13.168 | 17.5 | 5.98 | 18.5 | 2.203 | 0.2499 |
| D-081 | 0.5 | 3.2 | 2.4 | 4.1 | 13.699 | 5.5 | 2.47 | 3.5 | 5.552 | 0.0858 |
| D-082 | 0.5 | 3.2 | 2.4 | 4.1 | 13.093 | 7.9 | 3.71 | 5.5 | 3.533 | 0.117 |
| D-083 | 0.5 | 3.2 | 2.4 | 4.1 | 12.719 | 11.5 | 5.56 | 8.5 | 2.286 | 0.1638 |
| D-084 | 0.5 | 3.2 | 2.4 | 4.1 | 12.033 | 16 | 7.74 | 12.5 | 1.554 | 0.2262 |
| D-085 | 0.5 | 3.2 | 2.4 | 4.1 | 12.348 | 23.5 | 11.76 | 18.5 | 1.05 | 0.3199 |
| D-076 | 0.5 | 4 | 3.1 | 4.9 | 11.106 | 7 | 3.91 | 3.5 | 2.842 | 0.1073 |
| D-077 | 0.5 | 4 | 3.1 | 4.9 | 10.33 | 10 | 5.71 | 5.5 | 1.809 | 0.1463 |
| D-078 | 0.5 | 4 | 3.1 | 4.9 | 10.437 | 15 | 8.92 | 8.5 | 1.17 | 0.2048 |
| D-079 | 0.5 | 4 | 3.1 | 4.9 | 10.367 | 21.5 | 13.03 | 12.5 | 0.796 | 0.2828 |
| D-080 | 0.5 | 4 | 3.1 | 4.9 | 10.184 | 31 | 18.94 | 18.5 | 0.538 | 0.3998 |
| D-070 | 0.5 | 5 | 4.1 | 6.1 | 9.041 | 9.4 | 6.21 | 3.5 | 1.455 | 0.1341 |
| D-071 | 0.5 | 5 | 4.1 | 6.1 | 8.856 | 14 | 9.56 | 5.5 | 0.926 | 0.1828 |
| D-072 | 0.5 | 5 | 4.1 | 6.1 | 8.502 | 20.5 | 14.19 | 8.5 | 0.599 | 0.256 |
| D-073 | 0.5 | 5 | 4.1 | 6.1 | 8.634 | 30 | 21.19 | 12.5 | 0.408 | 0.3535 |
| D-074 | 0.5 | 5 | 4.1 | 6.1 | 8.794 | 44.5 | 31.94 | 18.5 | 0.275 | 0.4998 |
| D-064 | 0.5 | 6.3 | 5.4 | 7.5 | 7.391 | 13.5 | 10.16 | 3.5 | 0.728 | 0.169 |
| D-065 | 0.5 | 6.3 | 5.4 | 7.5 | 7.093 | 20 | 15.32 | 5.5 | 0.463 | 0.2304 |
| D-066 | 0.5 | 6.3 | 5.4 | 7.5 | 6.984 | 30 | 23.31 | 8.5 | 0.3 | 0.3225 |
| D-067 | 0.5 | 6.3 | 5.4 | 7.5 | 7.056 | 44 | 34.64 | 12.5 | 0.204 | 0.4454 |
| D-068 | 0.5 | 6.3 | 5.4 | 7.5 | 7.105 | 65 | 51.62 | 18.5 | 0.138 | 0.6297 |
| D-111 | 0.63 | 3.2 | 2.3 | 4.2 | 24.196 | 5.5 | 1.73 | 3.5 | 13.993 | 0.1362 |
| D-112 | 0.63 | 3.2 | 2.3 | 4.2 | 23.102 | 7.8 | 2.59 | 5.5 | 8.905 | 0.1858 |
| D-113 | 0.63 | 3.2 | 2.3 | 4.2 | 20.986 | 11 | 3.64 | 8.5 | 5.762 | 0.2601 |
| D-114 | 0.63 | 3.2 | 2.3 | 4.2 | 20.659 | 15.5 | 5.27 | 12.5 | 3.918 | 0.3592 |
| D-115 | 0.63 | 3.2 | 2.3 | 4.2 | 21.095 | 22.5 | 7.97 | 18.5 | 2.647 | 0.5078 |
| D-106 | 0.63 | 4 | 3 | 5 | 20.642 | 6.7 | 2.88 | 3.5 | 7.164 | 0.1703 |
| D-107 | 0.63 | 4 | 3 | 5 | 19.691 | 9.6 | 4.32 | 5.5 | 4.559 | 0.2322 |
| D-108 | 0.63 | 4 | 3 | 5 | 19.251 | 14 | 6.53 | 8.5 | 2.95 | 0.3251 |
| D-109 | 0.63 | 4 | 3 | 5 | 19.261 | 20 | 9.6 | 12.5 | 2.006 | 0.449 |
| D-110 | 0.63 | 4 | 3 | 5 | 19.267 | 29 | 14.21 | 18.5 | 1.355 | 0.6348 |
| D-101 | 0.63 | 5 | 4 | 6.1 | 16.896 | 8.5 | 4.61 | 3.5 | 3.668 | 0.2129 |
| D-102 | 0.63 | 5 | 4 | 6.1 | 16.576 | 12.5 | 7.1 | 5.5 | 2.334 | 0.2903 |
| D-103 | 0.63 | 5 | 4 | 6.1 | 16.378 | 18.5 | 10.84 | 8.5 | 1.51 | 0.4064 |
| D-104 | 0.63 | 5 | 4 | 6.1 | 15.749 | 26 | 15.33 | 12.5 | 1.027 | 0.5612 |
| D-105 | 0.63 | 5 | 4 | 6.1 | 16.182 | 38.5 | 23.32 | 18.5 | 0.694 | 0.7935 |
| D-096 | 0.63 | 6.3 | 5.2 | 7.5 | 13.723 | 11.5 | 7.48 | 3.5 | 1.834 | 0.2682 |
| D-097 | 0.63 | 6.3 | 5.2 | 7.5 | 13.313 | 17 | 11.41 | 5.5 | 1.167 | 0.3658 |
| D-098 | 0.63 | 6.3 | 5.2 | 7.5 | 13.249 | 25.5 | 17.55 | 8.5 | 0.755 | 0.5121 |
| D-099 | 0.63 | 6.3 | 5.2 | 7.5 | 13.04 | 36.5 | 25.4 | 12.5 | 0.513 | 0.7071 |
| D-100 | 0.63 | 6.3 | 5.2 | 7.5 | 13.243 | 54 | 38.17 | 18.5 | 0.347 | 0.9998 |
| D-091 | 0.63 | 8 | 6.9 | 9.4 | 10.551 | 16 | 11.78 | 3.5 | 0.896 | 0.3406 |
| D-092 | 0.63 | 8 | 6.9 | 9.4 | 10.595 | 24.5 | 18.59 | 5.5 | 0.57 | 0.4645 |
| D-093 | 0.63 | 8 | 6.9 | 9.4 | 10.53 | 37 | 28.55 | 8.5 | 0.369 | 0.6503 |
| D-094 | 0.63 | 8 | 6.9 | 9.4 | 10.826 | 55 | 43.17 | 12.5 | 0.251 | 0.898 |
| D-095 | 0.63 | 8 | 6.9 | 9.4 | 10.776 | 80.5 | 63.6 | 18.5 | 0.169 | 1.2695 |
| D-138 | 0.8 | 4 | 2.8 | 5.2 | 39.399 | 6.9 | 2.12 | 3.5 | 18.629 | 0.2746 |
| D-139 | 0.8 | 4 | 2.8 | 5.2 | 36.69 | 9.7 | 3.1 | 5.5 | 11.855 | 0.3745 |
| D-140 | 0.8 | 4 | 2.8 | 5.2 | 35.783 | 14 | 4.67 | 8.5 | 7.671 | 0.5243 |
| D-141 | 0.8 | 4 | 2.8 | 5.2 | 34.034 | 19.5 | 6.53 | 12.5 | 5.216 | 0.724 |
| D-142 | 0.8 | 4 | 2.8 | 5.2 | 33.71 | 28 | 9.57 | 18.5 | 3.524 | 1.0236 |
| D-133 | 0.8 | 5 | 3.8 | 6.3 | 32.962 | 8.3 | 3.46 | 3.5 | 9.538 | 0.3433 |
| D-134 | 0.8 | 5 | 3.8 | 6.3 | 32.182 | 12 | 5.3 | 5.5 | 6.07 | 0.4681 |
| D-135 | 0.8 | 5 | 3.8 | 6.3 | 31.503 | 17.5 | 8.02 | 8.5 | 3.927 | 0.6553 |
| D-136 | 0.8 | 5 | 3.8 | 6.3 | 30.215 | 24.5 | 11.31 | 12.5 | 2.671 | 0.905 |
| D-137 | 0.8 | 5 | 3.8 | 6.3 | 31.132 | 36 | 17.25 | 18.5 | 1.804 | 1.2795 |
| D-128 | 0.8 | 6.3 | 5.1 | 7.6 | 26.508 | 10.5 | 5.56 | 3.5 | 4.768 | 0.4325 |
| D-129 | 0.8 | 6.3 | 5.1 | 7.6 | 26.248 | 15.5 | 8.65 | 5.5 | 3.034 | 0.5898 |
| D-130 | 0.8 | 6.3 | 5.1 | 7.6 | 26.087 | 23 | 13.29 | 8.5 | 1.963 | 0.8257 |
| D-131 | 0.8 | 6.3 | 5.1 | 7.6 | 25.993 | 33 | 19.47 | 12.5 | 1.335 | 1.1403 |
| D-132 | 0.8 | 6.3 | 5.1 | 7.6 | 25.928 | 48 | 28.74 | 18.5 | 0.902 | 1.6121 |
| D-123 | 0.8 | 8 | 6.7 | 9.5 | 21.889 | 14.5 | 9.4 | 3.5 | 2.329 | 0.5492 |
| D-124 | 0.8 | 8 | 6.7 | 9.5 | 21.338 | 21.5 | 14.4 | 5.5 | 1.482 | 0.7489 |
| D-125 | 0.8 | 8 | 6.7 | 9.5 | 20.998 | 32 | 21.9 | 8.5 | 0.959 | 1.0485 |
| D-126 | 0.8 | 8 | 6.7 | 9.5 | 21.451 | 47 | 32.9 | 12.5 | 0.652 | 1.448 |
| D-127 | 0.8 | 8 | 6.7 | 9.5 | 21.102 | 68 | 47.9 | 18.5 | 0.441 | 2.0471 |
| D-118 | 0.8 | 10 | 8.7 | 11.6 | 17.483 | 20 | 14.66 | 3.5 | 1.192 | 0.6865 |
| D-119 | 0.8 | 10 | 8.7 | 11.6 | 17.092 | 30 | 22.53 | 5.5 | 0.759 | 0.9362 |
| D-120 | 0.8 | 10 | 8.7 | 11.6 | 17.136 | 45.58 | 34.91 | 8.5 | 0.491 | 1.3107 |
| D-121 | 0.8 | 10 | 8.7 | 11.6 | 17.044 | 66 | 51.06 | 12.5 | 0.334 | 1.81 |
| D-122 | 0.8 | 10 | 8.7 | 11.6 | 16.951 | 96.5 | 75.15 | 18.5 | 0.226 | 2.5589 |
| D-174 | 1 | 5 | 3.6 | 6.4 | 58.651 | 8.5 | 2.52 | 3.5 | 23.286 | 0.5364 |
| D-175 | 1 | 5 | 3.6 | 6.4 | 55.476 | 12 | 3.74 | 5.5 | 14.818 | 0.7314 |
| D-176 | 1 | 5 | 3.6 | 6.4 | 51.117 | 17 | 5.33 | 8.5 | 9.588 | 1.024 |
| D-177 | 1 | 5 | 3.6 | 6.4 | 50.734 | 24 | 7.78 | 12.5 | 6.52 | 1.414 |
| D-178 | 1 | 5 | 3.6 | 6.4 | 48.267 | 34 | 10.96 | 18.5 | 4.405 | 1.9991 |
| D-167 | 1 | 6.3 | 4.9 | 7.8 | 45.883 | 10 | 3.94 | 3.5 | 11.641 | 0.6758 |
| D-168 | 1 | 6.3 | 4.9 | 7.8 | 45.354 | 14.5 | 6.12 | 5.5 | 7.408 | 0.9216 |
| D-169 | 1 | 6.3 | 4.9 | 7.8 | 46.226 | 21.5 | 9.64 | 8.5 | 4.793 | 1.2902 |
| D-170 | 1 | 6.3 | 4.9 | 7.8 | 45.65 | 30.5 | 14.01 | 12.5 | 3.259 | 1.7817 |
| D-171 | 1 | 6.3 | 4.9 | 7.8 | 44.153 | 43.5 | 20.05 | 18.5 | 2.202 | 2.5189 |
| D-159 | 1 | 8 | 6.5 | 9.6 | 38.738 | 13 | 6.81 | 3.5 | 5.685 | 0.8582 |
| D-160 | 1 | 8 | 6.5 | 9.6 | 37.704 | 19 | 10.42 | 5.5 | 3.618 | 1.1702 |
| D-161 | 1 | 8 | 6.5 | 9.6 | 38.236 | 28.5 | 16.33 | 8.5 | 2.341 | 1.6383 |
| D-163 | 1 | 8 | 6.5 | 9.6 | 37.487 | 40.5 | 23.55 | 12.5 | 1.592 | 2.2624 |
| D-165 | 1 | 8 | 6.5 | 9.6 | 37.508 | 59 | 34.87 | 18.5 | 1.076 | 3.1986 |
| D-151 | 1 | 10 | 8.5 | 11.7 | 32.382 | 17.5 | 11.13 | 3.5 | 2.911 | 1.0727 |
| D-152 | 1 | 10 | 8.5 | 11.7 | 31.72 | 26 | 17.13 | 5.5 | 1.852 | 1.4628 |
| D-153 | 1 | 10 | 8.5 | 11.7 | 31.611 | 39 | 26.38 | 8.5 | 1.199 | 2.0479 |
| D-154 | 1 | 10 | 8.5 | 11.7 | 31.276 | 56 | 38.38 | 12.5 | 0.815 | 2.8281 |
| D-155 | 1 | 10 | 8.5 | 11.7 | 31.044 | 81.5 | 56.38 | 18.5 | 0.551 | 3.9983 |
| D-146 | 1 | 12.5 | 10.9 | 14.3 | 25.826 | 24 | 17.33 | 3.5 | 1.49 | 1.3409 |
| D-147 | 1 | 12.5 | 10.9 | 14.3 | 25.758 | 36.5 | 27.16 | 5.5 | 0.948 | 1.8285 |
| D-148 | 1 | 12.5 | 10.9 | 14.3 | 25.87 | 55.5 | 42.16 | 8.5 | 0.614 | 2.5599 |
| D-149 | 1 | 12.5 | 10.9 | 14.3 | 25.796 | 80.5 | 61.82 | 12.5 | 0.417 | 3.5351 |
| D-150 | 1 | 12.5 | 10.9 | 14.3 | 24.9 | 115 | 88.31 | 18.5 | 0.282 | 4.9979 |
| D-201 | 1.25 | 6.3 | 4.6 | 8.1 | 128.479 | 12 | 4.52 | 3.5 | 28.42 | 1.056 |
| D-202 | 1.25 | 6.3 | 4.6 | 8.1 | 120.729 | 17 | 6.68 | 5.5 | 18.085 | 1.4399 |
| D-203 | 1.25 | 6.3 | 4.6 | 8.1 | 121.792 | 25 | 10.41 | 8.5 | 11.702 | 2.0159 |
| D-204 | 1.25 | 6.3 | 4.6 | 8.1 | 121.09 | 35.5 | 15.22 | 12.5 | 7.957 | 2.7839 |
| D-205 | 1.25 | 6.3 | 4.6 | 8.1 | 121.951 | 51.5 | 22.68 | 18.5 | 5.377 | 3.9358 |
| D-196 | 1.25 | 8 | 6.3 | 9.8 | 102.967 | 15 | 7.42 | 3.5 | 13.879 | 1.3409 |
| D-197 | 1.25 | 8 | 6.3 | 9.8 | 101.705 | 22 | 11.52 | 5.5 | 8.832 | 1.8285 |
| D-198 | 1.25 | 8 | 6.3 | 9.8 | 103.156 | 33 | 18.05 | 8.5 | 5.715 | 2.5599 |
| D-199 | 1.25 | 8 | 6.3 | 9.8 | 103.179 | 47.5 | 26.55 | 12.5 | 3.886 | 3.5351 |
| D-200 | 1.25 | 8 | 6.3 | 9.8 | 103.064 | 69 | 39.25 | 18.5 | 2.626 | 4.9979 |
| D-191 | 1.25 | 10 | 8.3 | 11.9 | 82.788 | 20 | 11.65 | 3.5 | 7.106 | 1.6761 |
| D-192 | 1.25 | 10 | 8.3 | 11.9 | 82.755 | 29.5 | 18.3 | 5.5 | 4.522 | 2.2856 |
| D-193 | 1.25 | 10 | 8.3 | 11.9 | 82.809 | 44.5 | 28.3 | 8.5 | 2.926 | 3.1998 |
| D-194 | 1.25 | 10 | 8.3 | 11.9 | 82.773 | 64 | 41.6 | 12.5 | 1.99 | 4.4188 |
| D-195 | 1.25 | 10 | 8.3 | 11.9 | 82.816 | 93.5 | 61.6 | 18.5 | 1.344 | 6.2473 |
| D-186 | 1.25 | 12.5 | 10.7 | 14.6 | 66.219 | 27 | 18.2 | 3.5 | 3.638 | 2.0951 |
| D-187 | 1.25 | 12.5 | 10.7 | 14.6 | 66.219 | 41.5 | 28.6 | 5.5 | 2.315 | 2.857 |
| D-188 | 1.25 | 12.5 | 10.7 | 14.6 | 66.369 | 62.5 | 44.3 | 8.5 | 1.498 | 3.9998 |
| D-189 | 1.25 | 12.5 | 10.7 | 14.6 | 66.219 | 90.5 | 65 | 12.5 | 1.019 | 5.5235 |
| D-190 | 1.25 | 12.5 | 10.7 | 14.6 | 66.425 | 130 | 96.5 | 18.5 | 0.688 | 7.8092 |
| D-181 | 1.25 | 16 | 14.2 | 18.5 | 51.701 | 40.5 | 29.8 | 3.5 | 1.735 | 2.6818 |
| D-182 | 1.25 | 16 | 14.2 | 18.5 | 51.945 | 62 | 47.05 | 5.5 | 1.104 | 3.657 |
| D-183 | 1.25 | 16 | 14.2 | 18.5 | 51.9 | 94 | 72.65 | 8.5 | 0.714 | 5.1198 |
| D-184 | 1.25 | 16 | 14.2 | 18.5 | 51.881 | 140 | 106.8 | 12.5 | 0.486 | 7.0701 |
| D-185 | 1.25 | 16 | 14.2 | 18.5 | 52.024 | 205 | 158.5 | 18.5 | 0.328 | 9.9957 |
| D-228 | 1.6 | 8 | 5.9 | 10.1 | 183.678 | 14.5 | 4.93 | 3.5 | 37.257 | 2.1969 |
| D-229 | 1.6 | 8 | 5.9 | 10.1 | 196.548 | 21.5 | 8.29 | 5.5 | 23.709 | 2.9958 |
| D-230 | 1.6 | 8 | 5.9 | 10.1 | 196.827 | 31.5 | 12.83 | 8.5 | 15.341 | 4.1941 |
| D-231 | 1.6 | 8 | 5.9 | 10.1 | 198.73 | 45 | 19.05 | 12.5 | 10.432 | 5.7919 |
| D-232 | 1.6 | 8 | 5.9 | 10.1 | 201.803 | 65.5 | 28.63 | 18.5 | 7.049 | 8.1885 |
| D-223 | 1.6 | 10 | 7.9 | 12.2 | 165.958 | 18.5 | 8.7 | 3.5 | 19.076 | 2.7461 |
| D-224 | 1.6 | 10 | 7.9 | 12.2 | 165.144 | 27 | 13.6 | 5.5 | 12.139 | 3.7447 |
| D-225 | 1.6 | 10 | 7.9 | 12.2 | 166.362 | 40.5 | 21.18 | 8.5 | 7.855 | 5.2426 |
| D-226 | 1.6 | 10 | 7.9 | 12.2 | 167.179 | 58.5 | 31.3 | 12.5 | 5.341 | 7.2398 |
| D-227 | 1.6 | 10 | 7.9 | 12.2 | 166.01 | 85 | 46 | 18.5 | 3.609 | 10.2356 |
| D-218 | 1.6 | 12.5 | 10.4 | 14.7 | 133.316 | 24 | 13.65 | 3.5 | 9.767 | 3.4327 |
| D-219 | 1.6 | 12.5 | 10.4 | 14.7 | 133.316 | 36 | 21.45 | 5.5 | 6.215 | 4.6809 |
| D-220 | 1.6 | 12.5 | 10.4 | 14.7 | 133.517 | 53.5 | 33.2 | 8.5 | 4.022 | 6.5533 |
| D-221 | 1.6 | 12.5 | 10.4 | 14.7 | 133.179 | 78 | 48.7 | 12.5 | 2.735 | 9.0498 |
| D-222 | 1.6 | 12.5 | 10.4 | 14.7 | 133.408 | 115 | 72.2 | 18.5 | 1.848 | 12.7945 |
| D-213 | 1.6 | 16 | 13.8 | 18.6 | 104.087 | 34 | 22.35 | 3.5 | 4.657 | 4.3938 |
| D-214 | 1.6 | 16 | 13.8 | 18.6 | 104.172 | 51.1 | 35.15 | 5.5 | 2.964 | 5.9916 |
| D-215 | 1.6 | 16 | 13.8 | 18.6 | 103.841 | 77.5 | 54.15 | 8.5 | 1.918 | 8.3882 |
| D-216 | 1.6 | 16 | 13.8 | 18.6 | 104.19 | 110 | 79.9 | 12.5 | 1.304 | 11.5837 |
| D-217 | 1.6 | 16 | 13.8 | 18.6 | 104.056 | 165 | 118.1 | 18.5 | 0.881 | 16.377 |
| D-208 | 1.6 | 20 | 17.7 | 23 | 83.218 | 48 | 34.9 | 3.5 | 2.384 | 5.4923 |
| D-209 | 1.6 | 20 | 17.7 | 23 | 83.304 | 73.5 | 54.9 | 5.5 | 1.517 | 7.4895 |
| D-210 | 1.6 | 20 | 17.7 | 23 | 83.358 | 110 | 84.9 | 8.5 | 0.982 | 10.4853 |
| D-211 | 1.6 | 20 | 17.7 | 23 | 83.122 | 165 | 124.5 | 12.5 | 0.668 | 14.4797 |
| D-212 | 1.6 | 20 | 17.7 | 23 | 83.321 | 240 | 184.7 | 18.5 | 0.451 | 20.4712 |
| D-258 | 2 | 10 | 7.5 | 12.6 | 281.175 | 18 | 6.04 | 3.5 | 46.571 | 4.2908 |
| D-259 | 2 | 10 | 7.5 | 12.6 | 295.993 | 26.5 | 9.99 | 5.5 | 29.636 | 5.8512 |
| D-260 | 2 | 10 | 7.5 | 12.6 | 290.763 | 38.5 | 15.16 | 8.5 | 19.176 | 8.1916 |
| D-261 | 2 | 10 | 7.5 | 12.6 | 294.215 | 55 | 22.56 | 12.5 | 13.04 | 11.3122 |
| D-262 | 2 | 10 | 7.5 | 12.6 | 294.391 | 79.5 | 33.41 | 18.5 | 8.811 | 15.9932 |
| D-253 | 2 | 12.5 | 10 | 15.2 | 247.741 | 22.5 | 10.39 | 3.5 | 23.845 | 5.3636 |
| D-254 | 2 | 12.5 | 10 | 15.2 | 246.658 | 33 | 16.26 | 5.5 | 15.174 | 7.3139 |
| D-255 | 2 | 12.5 | 10 | 15.2 | 250.368 | 49.5 | 25.5 | 8.5 | 9.818 | 10.2395 |
| D-256 | 2 | 12.5 | 10 | 15.2 | 250.368 | 71 | 37.5 | 12.5 | 6.676 | 14.1403 |
| D-257 | 2 | 12.5 | 10 | 15.2 | 250.368 | 105 | 55.5 | 18.5 | 4.511 | 19.9914 |
| D-248 | 2 | 16 | 13.5 | 18.6 | 195.564 | 30 | 17.2 | 3.5 | 11.37 | 6.8654 |
| D-249 | 2 | 16 | 13.5 | 18.6 | 195.357 | 45 | 27 | 5.5 | 7.235 | 9.3618 |
| D-250 | 2 | 16 | 13.5 | 18.6 | 194.995 | 68 | 41.65 | 8.5 | 4.682 | 13.1066 |
| D-251 | 2 | 16 | 13.5 | 18.6 | 195.313 | 98 | 61.35 | 12.5 | 3.184 | 18.0996 |
| D-252 | 2 | 16 | 13.5 | 18.6 | 195.21 | 145 | 90.75 | 18.5 | 2.151 | 25.589 |
| D-240 | 2 | 20 | 17.3 | 23.1 | 156.014 | 41 | 26.8 | 3.5 | 5.821 | 8.5817 |
| D-241 | 2 | 20 | 17.3 | 23.1 | 156.147 | 62 | 42.15 | 5.5 | 3.705 | 11.7023 |
| D-242 | 2 | 20 | 17.3 | 23.1 | 156.288 | 94 | 65.2 | 8.5 | 2.397 | 16.3832 |
| D-243 | 2 | 20 | 17.3 | 23.1 | 156.48 | 135 | 96 | 12.5 | 1.63 | 22.6245 |
| D-244 | 2 | 20 | 17.3 | 23.1 | 156.557 | 200 | 142.15 | 18.5 | 1.101 | 31.9863 |
| D-235 | 2 | 25 | 22.3 | 28.6 | 125.184 | 58 | 42 | 3.5 | 2.981 | 10.7271 |
| D-236 | 2 | 25 | 22.3 | 28.6 | 125.184 | 88.5 | 66 | 5.5 | 1.897 | 14.6279 |
| D-237 | 2 | 25 | 22.3 | 28.6 | 125.245 | 135 | 102.05 | 8.5 | 1.227 | 20.479 |
| D-238 | 2 | 25 | 22.3 | 28.6 | 125.184 | 195 | 150 | 12.5 | 0.835 | 28.2806 |
| D-239 | 2 | 25 | 22.3 | 28.6 | 125.212 | 290 | 222.05 | 18.5 | 0.564 | 39.9829 |
| D-284 | 2.5 | 12.5 | 9.4 | 15.7 | 410.229 | 22 | 7.05 | 3.5 | 58.214 | 8.3806 |
| D-285 | 2.5 | 12.5 | 9.4 | 15.7 | 420.813 | 32 | 11.36 | 5.5 | 37.045 | 11.428 |
| D-286 | 2.5 | 12.5 | 9.4 | 15.7 | 439.336 | 47.5 | 18.33 | 8.5 | 23.971 | 15.9992 |
| D-287 | 2.5 | 12.5 | 9.4 | 15.7 | 439.336 | 67.5 | 26.95 | 12.5 | 16.3 | 22.0942 |
| D-288 | 2.5 | 12.5 | 9.4 | 15.7 | 444.843 | 98 | 40.39 | 18.5 | 11.014 | 31.2366 |
| D-279 | 2.5 | 16 | 12.9 | 19.3 | 342.471 | 27.5 | 12.34 | 3.5 | 27.759 | 10.7271 |
| D-280 | 2.5 | 16 | 12.9 | 19.3 | 353.826 | 41 | 20.03 | 5.5 | 17.665 | 14.6279 |
| D-281 | 2.5 | 16 | 12.9 | 19.3 | 357.983 | 61 | 31.32 | 8.5 | 11.43 | 20.479 |
| D-282 | 2.5 | 16 | 12.9 | 19.3 | 363.012 | 88 | 46.71 | 12.5 | 7.772 | 28.2806 |
| D-283 | 2.5 | 16 | 12.9 | 19.3 | 366.04 | 130 | 69.7 | 18.5 | 5.252 | 39.9829 |
| D-274 | 2.5 | 20 | 16.8 | 23.3 | 291.853 | 36 | 20.54 | 3.5 | 14.212 | 13.4089 |
| D-275 | 2.5 | 20 | 16.8 | 23.3 | 292.131 | 54 | 32.3 | 5.5 | 9.044 | 18.2849 |
| D-276 | 2.5 | 20 | 16.8 | 23.3 | 292.61 | 81.5 | 50 | 8.5 | 5.852 | 25.5988 |
| D-277 | 2.5 | 20 | 16.8 | 23.3 | 293.289 | 120 | 73.7 | 12.5 | 3.979 | 35.3507 |
| D-278 | 2.5 | 20 | 16.8 | 23.3 | 292.546 | 175 | 108.8 | 18.5 | 2.689 | 49.9786 |
| D-269 | 2.5 | 25 | 21.8 | 28.8 | 234.313 | 49 | 32.2 | 3.5 | 7.277 | 16.7611 |
| D-270 | 2.5 | 25 | 21.8 | 28.8 | 233.849 | 74.5 | 50.5 | 5.5 | 4.631 | 22.8561 |
| D-271 | 2.5 | 25 | 21.8 | 28.8 | 233.713 | 115 | 78 | 8.5 | 2.996 | 31.9985 |
| D-272 | 2.5 | 25 | 21.8 | 28.8 | 234.72 | 165 | 115.2 | 12.5 | 2.038 | 44.1884 |
| D-273 | 2.5 | 25 | 21.8 | 28.8 | 235.001 | 240 | 170.7 | 18.5 | 1.377 | 62.4732 |
| D-264 | 2.5 | 32 | 28.7 | 35.3 | 182.514 | 71.5 | 52.6 | 3.5 | 3.47 | 21.4542 |
| D-265 | 2.5 | 32 | 28.7 | 35.3 | 183.271 | 110 | 83 | 5.5 | 2.208 | 29.2558 |
| D-266 | 2.5 | 32 | 28.7 | 35.3 | 182.881 | 170 | 128 | 8.5 | 1.429 | 40.9581 |
| D-267 | 2.5 | 32 | 28.7 | 35.3 | 182.652 | 245 | 188 | 12.5 | 0.972 | 56.5611 |
| D-268 | 2.5 | 32 | 28.7 | 35.5 | 183.283 | 360 | 279.2 | 18.5 | 0.656 | 79.9658 |
| D-309 | 3.2 | 16 | 12.1 | 20.1 | 622.939 | 27.5 | 8.36 | 3.5 | 74.514 | 17.5753 |
| D-310 | 3.2 | 16 | 12.1 | 20.1 | 643.939 | 40 | 13.58 | 5.5 | 47.418 | 23.9663 |
| D-311 | 3.2 | 16 | 12.1 | 20.1 | 664.58 | 59 | 21.66 | 8.5 | 30.682 | 33.5529 |
| D-312 | 3.2 | 16 | 12.1 | 20.1 | 659.302 | 83.5 | 31.6 | 12.5 | 20.864 | 46.3349 |
| D-313 | 3.2 | 16 | 12.1 | 20.1 | 652.141 | 120 | 46.26 | 18.5 | 14.097 | 65.5079 |
| D-304 | 3.2 | 20 | 16.1 | 24.2 | 538.84 | 33.5 | 14.12 | 3.5 | 38.151 | 21.9691 |
| D-305 | 3.2 | 20 | 16.1 | 24.2 | 551.326 | 49.5 | 22.71 | 5.5 | 24.278 | 29.9579 |
| D-306 | 3.2 | 20 | 16.1 | 24.2 | 566.892 | 74 | 36.09 | 8.5 | 15.709 | 41.9411 |
| D-307 | 3.2 | 20 | 16.1 | 24.2 | 558.22 | 105 | 52.26 | 12.5 | 10.682 | 57.9186 |
| D-308 | 3.2 | 20 | 16.1 | 24.2 | 577.506 | 155 | 80.01 | 18.5 | 7.218 | 81.8849 |
| D-299 | 3.2 | 25 | 21 | 29.3 | 444.477 | 42.5 | 22.75 | 3.5 | 19.533 | 27.4614 |
| D-300 | 3.2 | 25 | 21 | 29.3 | 449.094 | 63.5 | 36.13 | 5.5 | 12.43 | 37.4474 |
| D-301 | 3.2 | 25 | 21 | 29.3 | 447.924 | 94.5 | 55.69 | 8.5 | 8.043 | 52.4263 |
| D-302 | 3.2 | 25 | 21 | 29.3 | 442.679 | 135 | 80.94 | 12.5 | 5.469 | 72.3983 |
| D-303 | 3.2 | 25 | 21 | 29.3 | 454.771 | 200 | 123.06 | 18.5 | 3.696 | 102.3562 |
| D-294 | 3.2 | 32 | 27.8 | 36.9 | 354.874 | 58.5 | 38.1 | 3.5 | 9.314 | 35.1506 |
| D-295 | 3.2 | 32 | 27.8 | 36.9 | 356.229 | 88.5 | 60.1 | 5.5 | 5.927 | 47.9326 |
| D-296 | 3.2 | 32 | 27.8 | 36.9 | 362.819 | 135 | 94.6 | 8.5 | 3.835 | 67.1057 |
| D-297 | 3.2 | 32 | 27.8 | 36.9 | 348.429 | 190 | 133.6 | 12.5 | 2.608 | 92.6698 |
| D-298 | 3.2 | 32 | 27.8 | 36.9 | 351.728 | 280 | 199.6 | 18.5 | 1.762 | 131.0159 |
| D-289D | 3.2 | 40 | 35.8 | 45.3 | 289.258 | 82 | 60.66 | 3.5 | 4.769 | 43.9383 |
| D-290 | 3.2 | 40 | 35.8 | 45.3 | 288.652 | 125 | 95.12 | 5.5 | 3.035 | 59.9158 |
| D-291 | 3.2 | 40 | 35.8 | 45.3 | 289.258 | 190 | 147.31 | 8.5 | 1.964 | 83.8821 |
| D-292 | 3.2 | 40 | 35.8 | 45.3 | 287.389 | 275 | 215.23 | 12.5 | 1.335 | 115.8372 |
| D-293 | 3.2 | 40 | 35.8 | 45.3 | 288.356 | 405 | 319.61 | 18.5 | 0.902 | 163.7699 |
| D-335 | 4 | 20 | 15.2 | 25.1 | 891.843 | 33.5 | 9.58 | 3.5 | 93.143 | 34.3268 |
| D-336 | 4 | 20 | 15.2 | 25.1 | 946.882 | 49 | 15.98 | 5.5 | 59.273 | 46.8092 |
| D-337 | 4 | 20 | 15.2 | 25.1 | 971.288 | 72 | 25.33 | 8.5 | 38.353 | 65.5329 |
| D-338 | 4 | 20 | 15.2 | 25.1 | 1046.46 | 105 | 40.13 | 12.5 | 26.08 | 90.4978 |
| D-339 | 4 | 20 | 15.2 | 25.1 | 1018.97 | 150 | 57.83 | 18.5 | 17.622 | 127.9452 |
| D-330 | 4 | 25 | 20.3 | 30 | 800.209 | 41 | 16.78 | 3.5 | 47.689 | 42.9085 |
| D-331 | 4 | 25 | 20.3 | 30 | 819.718 | 60.5 | 27.01 | 5.5 | 30.348 | 58.5115 |
| D-332 | 4 | 25 | 20.3 | 30 | 826.859 | 89.5 | 42.11 | 8.5 | 19.637 | 81.9161 |
| D-333 | 4 | 25 | 20.3 | 30 | 855.528 | 130 | 64.07 | 12.5 | 13.353 | 113.1223 |
| D-334 | 4 | 25 | 20.3 | 30 | 823.409 | 185 | 91.26 | 18.5 | 9.022 | 159.9315 |
| D-325 | 4 | 32 | 27.1 | 37.1 | 653.91 | 53.5 | 28.76 | 3.5 | 22.74 | 54.9228 |
| D-326 | 4 | 32 | 27.1 | 37.1 | 653.91 | 79.5 | 45.19 | 5.5 | 14.471 | 74.8948 |
| D-327 | 4 | 32 | 27.1 | 37.1 | 667.955 | 120 | 71.34 | 8.5 | 9.364 | 104.8527 |
| D-328 | 4 | 32 | 27.1 | 37.1 | 650.727 | 170 | 102.2 | 12.5 | 6.367 | 144.7965 |
| D-329 | 4 | 32 | 27.1 | 37.1 | 660.363 | 250 | 153.5 | 18.5 | 4.302 | 204.7123 |
| D-319 | 4 | 40 | 34.9 | 45.8 | 529.75 | 71 | 45.5 | 3.5 | 11.643 | 68.6535 |
| D-320 | 4 | 40 | 34.9 | 45.8 | 514.932 | 105 | 69.5 | 5.5 | 7.409 | 93.6184 |
| D-321 | 4 | 40 | 34.9 | 45.8 | 524.956 | 160 | 109.5 | 8.5 | 4.794 | 131.0658 |
| D-322 | 4 | 40 | 34.9 | 45.8 | 536.27 | 235 | 164.5 | 12.5 | 3.26 | 180.9957 |
| D-323 | 4 | 40 | 34.9 | 45.8 | 527.547 | 340 | 239.5 | 18.5 | 2.203 | 255.8904 |
| D-314 | 4 | 50 | 44.8 | 56.2 | 431.102 | 99 | 72.32 | 3.5 | 5.961 | 85.8169 |
| D-315 | 4 | 50 | 44.8 | 56.2 | 427.309 | 150 | 112.64 | 5.5 | 3.793 | 117.0231 |
| D-316 | 4 | 50 | 44.8 | 56.2 | 433.557 | 230 | 176.63 | 8.5 | 2.455 | 163.8323 |
| D-317 | 4 | 50 | 44.8 | 56.2 | 434.441 | 335 | 260.28 | 12.5 | 1.669 | 226.2446 |
| D-318 | 4 | 50 | 44.8 | 56.2 | 432.23 | 490 | 383.26 | 18.5 | 1.128 | 319.863 |
| D-360 | 5 | 25 | 19.1 | 31 | 1291.629 | 41 | 11.09 | 3.5 | 116.429 | 67.0445 |
| D-361 | 5 | 25 | 19.1 | 31 | 1386.889 | 60 | 18.72 | 5.5 | 74.091 | 91.4243 |
| D-362 | 5 | 25 | 19.1 | 31 | 1397.785 | 87.5 | 29.16 | 8.5 | 47.941 | 127.994 |
| D-363 | 5 | 25 | 19.1 | 31 | 1431.344 | 125 | 43.91 | 12.5 | 32.6 | 176.7536 |
| D-364 | 5 | 25 | 19.1 | 31 | 1426.938 | 180 | 64.78 | 18.5 | 22.027 | 249.893 |
| D-355 | 5 | 32 | 26 | 38.2 | 1147.813 | 51 | 20.67 | 3.5 | 55.517 | 85.8169 |
| D-356 | 5 | 32 | 26 | 38.2 | 1168.001 | 75 | 33.06 | 5.5 | 35.329 | 117.0231 |
| D-357 | 5 | 32 | 26 | 38.2 | 1157.61 | 110 | 50.64 | 8.5 | 22.86 | 163.8323 |
| D-358 | 5 | 32 | 26 | 38.2 | 1203.33 | 160 | 77.41 | 12.5 | 15.545 | 226.2446 |
| D-359 | 5 | 32 | 26 | 38.2 | 1182.323 | 230 | 112.57 | 18.5 | 10.503 | 319.863 |
| D-350 | 5 | 40 | 34 | 46.5 | 940.013 | 64 | 33.07 | 3.5 | 28.425 | 107.2711 |
| D-351 | 5 | 40 | 34 | 46.5 | 951.641 | 95.5 | 52.61 | 5.5 | 18.089 | 146.2788 |
| D-352 | 5 | 40 | 34 | 46.5 | 926.636 | 140 | 79.17 | 8.5 | 11.704 | 204.7904 |
| D-353 | 5 | 40 | 34 | 46.5 | 957.068 | 205 | 120.25 | 12.5 | 7.959 | 282.8057 |
| D-354 | 5 | 40 | 34 | 46.5 | 964.597 | 300 | 179.37 | 18.5 | 5.378 | 399.8288 |
| D-345 | 5 | 50 | 43.7 | 56.8 | 773.158 | 85 | 53.13 | 3.5 | 14.554 | 134.0889 |
| D-346 | 5 | 50 | 43.7 | 56.8 | 793.004 | 130 | 85.63 | 5.5 | 9.261 | 182.8485 |
| D-347 | 5 | 50 | 43.7 | 56.8 | 790.28 | 195 | 131.88 | 8.5 | 5.993 | 255.9879 |
| D-348 | 5 | 50 | 43.7 | 56.8 | 781.891 | 280 | 191.88 | 12.5 | 4.075 | 353.5072 |
| D-349 | 5 | 50 | 43.7 | 56.8 | 782.992 | 410 | 284.38 | 18.5 | 2.753 | 499.786 |
| D-340 | 5 | 63 | 56.5 | 71 | 629.924 | 120 | 86.58 | 3.5 | 7.275 | 168.952 |
| D-341 | 5 | 63 | 56.5 | 71 | 616.696 | 180 | 133.2 | 5.5 | 4.63 | 230.3891 |
| D-342 | 5 | 63 | 56.5 | 71 | 623.505 | 275 | 208.13 | 8.5 | 2.996 | 322.5448 |
| D-343 | 5 | 63 | 56.5 | 71 | 613.918 | 395 | 301.37 | 12.5 | 2.037 | 445.419 |
| D-344 | 5 | 63 | 56.5 | 71 | 621.076 | 585 | 451.22 | 18.5 | 1.376 | 629.7303 |
| D-385 | 6.3 | 32 | 24.7 | 39.6 | 1719.977 | 50 | 12.29 | 3.5 | 139.93 | 136.2429 |
| D-386 | 6.3 | 32 | 24.7 | 39.6 | 2043.089 | 75 | 22.94 | 5.5 | 89.047 | 185.7858 |
| D-387 | 6.3 | 32 | 24.7 | 39.6 | 2098.612 | 110 | 36.42 | 8.5 | 57.618 | 260.1001 |
| D-388 | 6.3 | 32 | 24.7 | 39.6 | 2065.885 | 155 | 52.73 | 12.5 | 39.18 | 359.1859 |
| D-389 | 6.3 | 32 | 24.7 | 39.6 | 2109.513 | 225 | 79.68 | 18.5 | 26.473 | 507.8145 |
| D-380 | 6.3 | 40 | 32.7 | 47.5 | 1562.682 | 60 | 21.81 | 3.5 | 71.644 | 170.3037 |
| D-381 | 6.3 | 40 | 32.7 | 47.5 | 1695.55 | 90 | 37.19 | 5.5 | 45.592 | 232.2323 |
| D-382 | 6.3 | 40 | 32.7 | 47.5 | 1777.615 | 135 | 60.26 | 8.5 | 29.501 | 325.1252 |
| D-383 | 6.3 | 40 | 32.7 | 47.5 | 1825.76 | 195 | 91.01 | 12.5 | 20.06 | 448.9824 |
| D-384 | 6.3 | 40 | 32.7 | 47.5 | 1791.169 | 280 | 132.15 | 18.5 | 13.554 | 634.7682 |
| D-375 | 6.3 | 50 | 42.6 | 57.7 | 1506.22 | 80 | 41.06 | 3.5 | 36.682 | 212.8796 |
| D-376 | 6.3 | 50 | 42.6 | 57.7 | 1424.186 | 115 | 61.01 | 5.5 | 23.343 | 290.2903 |
| D-377 | 6.3 | 50 | 42.6 | 57.7 | 1486.8 | 175 | 98.44 | 8.5 | 15.104 | 406.4065 |
| D-378 | 6.3 | 50 | 42.6 | 57.7 | 1472.179 | 250 | 143.33 | 12.5 | 10.271 | 561.228 |
| D-379 | 6.3 | 50 | 42.6 | 57.7 | 1479.452 | 365 | 213.18 | 18.5 | 6.94 | 793.4602 |
| D-370 | 6.3 | 63 | 55 | 72 | 1188.958 | 105 | 64.84 | 3.5 | 18.338 | 268.2283 |
| D-371 | 6.3 | 63 | 55 | 72 | 1156.284 | 155 | 99.09 | 5.5 | 11.669 | 365.7658 |
| D-372 | 6.3 | 63 | 55 | 72 | 1173.856 | 235 | 155.46 | 8.5 | 7.551 | 512.0721 |
| D-373 | 6.3 | 63 | 55 | 72 | 1175.608 | 340 | 228.96 | 12.5 | 5.135 | 707.1472 |
| D-374 | 6.3 | 63 | 55 | 72 | 1185.488 | 500 | 341.71 | 18.5 | 3.469 | 999.7599 |
| D-365 | 6.3 | 80 | 72 | 88.7 | 920.734 | 145 | 102.81 | 3.5 | 8.956 | 340.6073 |
| D-366 | 6.3 | 80 | 72 | 88.7 | 916.989 | 220 | 160.9 | 5.5 | 5.699 | 464.4645 |
| D-367 | 6.3 | 80 | 72 | 88.7 | 967.989 | 355 | 262.5 | 8.5 | 3.688 | 650.2503 |
| D-368 | 6.3 | 80 | 72 | 88.7 | 932.126 | 490 | 371.73 | 12.5 | 2.508 | 897.9647 |
| D-369 | 6.3 | 80 | 72 | 88.7 | 933.562 | 720 | 551 | 18.5 | 1.694 | 1269.5364 |
| D-410 | 8 | 40 | 30.8 | 49.3 | 3194.8 | 65 | 17.15 | 3.5 | 186.286 | 274.6141 |
| D-411 | 8 | 40 | 30.8 | 49.3 | 2839.164 | 90 | 23.95 | 5.5 | 118.545 | 374.4738 |
| D-412 | 8 | 40 | 30.8 | 49.3 | 3194.8 | 135 | 41.65 | 8.5 | 76.706 | 524.2633 |
| D-413 | 8 | 40 | 30.8 | 49.3 | 3142.64 | 190 | 60.25 | 12.5 | 52.16 | 723.9827 |
| D-414 | 8 | 40 | 30.8 | 49.3 | 3194.8 | 275 | 90.65 | 18.5 | 35.243 | 1023.5617 |
| D-405 | 8 | 50 | 40.8 | 59.5 | 2533.188 | 75 | 26.56 | 3.5 | 95.378 | 343.2676 |
| D-406 | 8 | 50 | 40.8 | 59.5 | 2611.224 | 110 | 43.02 | 5.5 | 60.695 | 468.0922 |
| D-407 | 8 | 50 | 40.8 | 59.5 | 2561.24 | 160 | 65.22 | 8.5 | 39.273 | 655.3291 |
| D-408 | 8 | 50 | 40.8 | 59.5 | 2620.936 | 230 | 98.14 | 12.5 | 26.706 | 904.9783 |
| D-409 | 8 | 50 | 40.8 | 59.5 | 2752.3 | 340 | 152.53 | 18.5 | 18.045 | 1279.4521 |
| D-400 | 8 | 63 | 53.6 | 73.1 | 2173.994 | 95 | 45.6 | 3.5 | 47.68 | 432.5172 |
| D-401 | 8 | 63 | 53.6 | 73.1 | 2169.66 | 140 | 71.51 | 5.5 | 30.342 | 589.7962 |
| D-402 | 8 | 63 | 53.6 | 73.1 | 2117.9 | 205 | 107.87 | 8.5 | 19.633 | 825.7147 |
| D-403 | 8 | 63 | 53.6 | 73.1 | 2198.788 | 300 | 164.7 | 12.5 | 13.35 | 1140.2727 |
| D-404 | 8 | 63 | 53.6 | 73.1 | 2186.881 | 435 | 242.43 | 18.5 | 9.021 | 1612.1097 |
| D-395 | 8 | 80 | 70 | 90.8 | 1723.143 | 125 | 74 | 3.5 | 23.286 | 549.2282 |
| D-396 | 8 | 80 | 70 | 90.8 | 1615.182 | 180 | 109 | 5.5 | 14.818 | 748.9476 |
| D-397 | 8 | 80 | 70 | 90.8 | 1764.235 | 285 | 184 | 8.5 | 9.588 | 1048.5266 |
| D-398 | 8 | 80 | 70 | 90.8 | 1753.88 | 410 | 269 | 12.5 | 6.52 | 1447.9653 |
| D-399 | 8 | 80 | 70 | 90.8 | 1757.757 | 600 | 399 | 18.5 | 4.405 | 2047.1234 |
| D-390 | 8 | 100 | 89 | 111 | 1390.586 | 170 | 116.64 | 3.5 | 11.922 | 686.5353 |
| D-391 | 8 | 100 | 89 | 111 | 1405.759 | 260 | 185.29 | 5.5 | 7.587 | 936.1845 |
| D-392 | 8 | 100 | 89 | 111 | 1390.586 | 390 | 283.26 | 8.5 | 4.909 | 1310.6583 |
| D-393 | 8 | 100 | 89 | 111 | 1403.939 | 570 | 420.56 | 12.5 | 3.338 | 1809.9567 |
| D-394 | 8 | 100 | 89 | 111 | 1401.863 | 835 | 621.51 | 18.5 | 2.256 | 2558.9042 |
| D-435 | 10 | 50 | 38 | 62 | 3536.518 | 75 | 15.19 | 3.5 | 232.857 | 536.3557 |
| D-436 | 10 | 50 | 38 | 62 | 4065.739 | 110 | 27.44 | 5.5 | 148.182 | 731.3941 |
| D-437 | 10 | 50 | 38 | 62 | 4632.316 | 165 | 48.31 | 8.5 | 95.882 | 1023.9518 |
| D-438 | 10 | 50 | 38 | 62 | 4421.375 | 230 | 67.81 | 12.5 | 65.2 | 1414.0286 |
| D-439 | 10 | 50 | 38 | 62 | 4606.402 | 335 | 104.56 | 18.5 | 44.054 | 1999.1439 |
| D-430 | 10 | 63 | 51 | 75 | 4122.691 | 96 | 35.42 | 3.5 | 116.407 | 675.8082 |
| D-431 | 10 | 63 | 51 | 75 | 3794.636 | 135 | 51.23 | 5.5 | 74.077 | 921.5566 |
| D-432 | 10 | 63 | 51 | 75 | 3903.573 | 200 | 81.44 | 8.5 | 47.932 | 1290.1792 |
| D-433 | 10 | 63 | 51 | 75 | 3913.159 | 285 | 120.06 | 12.5 | 32.594 | 1781.6761 |
| D-434 | 10 | 63 | 51 | 75 | 3864.709 | 410 | 175.49 | 18.5 | 22.023 | 2518.9214 |
| D-425 | 10 | 80 | 68 | 93 | 3021.003 | 115 | 53.14 | 3.5 | 56.85 | 858.1691 |
| D-426 | 10 | 80 | 68 | 93 | 3227.73 | 175 | 89.22 | 5.5 | 36.177 | 1170.2306 |
| D-427 | 10 | 80 | 68 | 93 | 3121.326 | 255 | 133.34 | 8.5 | 23.409 | 1638.3228 |
| D-428 | 10 | 80 | 68 | 93 | 3191.553 | 370 | 200.5 | 12.5 | 15.918 | 2262.4458 |
| D-429 | 10 | 80 | 68 | 93 | 3213.064 | 540 | 298.74 | 18.5 | 10.755 | 3198.6303 |
| D-420 | 10 | 100 | 88 | 114 | 2510.491 | 150 | 86.25 | 3.5 | 29.107 | 1072.7114 |
| D-421 | 10 | 100 | 88 | 114 | 2616.335 | 230 | 141.25 | 5.5 | 18.523 | 1462.7882 |
| D-422 | 10 | 100 | 88 | 114 | 2621.783 | 345 | 218.75 | 8.5 | 11.985 | 2047.9035 |
| D-423 | 10 | 100 | 88 | 114 | 2638.563 | 500 | 323.75 | 12.5 | 8.15 | 2828.0573 |
| D-424 | 10 | 100 | 88 | 114 | 2636.36 | 730 | 478.75 | 18.5 | 5.507 | 3998.2879 |
| D-415 | 10 | 125 | 112 | 140 | 2061.019 | 205 | 138.3 | 3.5 | 14.903 | 1340.8892 |
| D-416 | 10 | 125 | 112 | 140 | 2101.663 | 315 | 221.61 | 5.5 | 9.484 | 1828.4853 |
| D-417 | 10 | 125 | 112 | 140 | 2096.084 | 475 | 341.58 | 8.5 | 6.136 | 2559.8794 |
| D-418 | 10 | 125 | 112 | 140 | 2099.766 | 690 | 503.2 | 12.5 | 4.173 | 3535.0716 |
| D-419 | 10 | 125 | 112 | 140 | 2109.352 | 1015 | 748.14 | 18.5 | 2.819 | 4997.8598 |
Unter Kugelstrahlen versteht man eine besondere Art der Oberflächenbearbeitung. Bei dem Verfahren werden Strahlmittel in speziellen Anlagen beschleunigt und zum Aufprall auf die Oberfläche der zu bearbeitenden Werkstücke, wie zum Beispiel Metallfedern, gelenkt. Das Strahlmittel besteht aus runden oder gerundeten Körnern, denen der Vorgang seinen Namen verdankt.
In der Regel tritt die höchste Beanspruchung von Metallfedern an der Werkstoffoberfläche auf. Kleine Fehler wie Kratzer, Haarrisse, Entkohlungen oder Riefen sind da keine Seltenheit. Diese können sich jedoch negativ auf die Leistung und die Lebensdauer der Federn auswirken. Mit der Verfestigung der Randschichten wird deshalb versucht, Fehler zu minimieren und die Dauerfestigkeit der Federn zu steigern. Übliche Verfahren im Maschinenbau sind zum Beispiel Oberflächen-Festwalzen, Randschichthärtung oder Randschichtnitrieren. Weil Metallfedern eine besondere und komplizierte Geometrie aufweisen, hat sich für diese Werkstücke im Lauf der Zeit jedoch nur das Kugelstrahl-Verfahren durchgesetzt. Die Dauerfestigkeit lässt sich steigern, indem in den Randschichten des Federwerkstoffs Druckspannungen erzeugt, die dünnen Randschichten kaltverfestigt und die Oberflächen geglättet werden. Damit lassen sich Oberflächenfehler erheblich reduzieren.
Ziel des Kugelstrahlens ist es, durch Umformung und damit durch Verfestigung der Oberfläche Druckeigenspannungen aufzubauen. Mit dem Verfahren lässt sich somit die Dauerhaltbarkeit von Metallfedern deutlich verbessern. Dazu werden Stahlkugeln oder gerundetes Drahtkorn durch Pressluft oder Schleuderräder mit einer hohen Geschwindigkeit auf die Federn geschossen. Durch den Vorgang wird das Oberflächenvolumen des Werkstoffs vergrößert und eine Druckeigenspannung erzeugt. Die Folge ist eine Verdichtung des Werkstoffs und damit die Verfestigung der Oberfläche, die durch die Behandlung besonders korrosionsbeständig wird und keine Risse zulässt. Der Verdichtungsgrad ist abhängig von den Strahlenbedingungen wie der Abwurfgeschwindigkeit, Behandlungsdauer oder dem Strahlwinkel sowie Korndurchmesser, -festigkeit und -zustand des Strahlmittels. Eine wichtige Rolle für die Verdichtung spielt außerdem die Härte des Federwerkstoffs. Aufgrund des hohen Korrosionsschutzes ist das Kugelstrahlen zudem eine gute Vorbereitung für nachfolgende Behandlungen wie die Oberflächenveredelung.

Die Abbildung zeigt ein Dauerfestigkeitsdiagramm – oder auch Wöhlerkurven genannt – für Druckfedern aus patentiert gezogenem (blaue Kurven 1) und vergütetem Ventilfederdraht (orangene Kurven 2). Die Steigerung der Zeit- und Dauerfestigkeit kugelgestrahlter (Kurve 1k und 2k) gegenüber ungestrahlter (Kurve 1 und 2) Federn ist deutlich erkennbar. Beim Kugelstrahlen entstehen umvermeidbare Spannungsspitzen in Oberflächennähe. Diese führen gegenüber ungestrahlten Federn zu einer größeren Relaxation. Sie kann durch ein Entspannen nach dem Strahlen bei einer Temperatur von 200 bis 240 °C vermieden werden. Um die Steigerung der Dauerfestigkeit langfristig zu erhalten, gilt es, werkstoffabhängige Temperaturgrenzen einzuhalten.
Zu den häufigsten Fehlern gehört das Strahlen mit scharfkantigen oder gebrochenen Körnern. Das kann zur Folge haben, dass die Dauerfestigkeit durch die Kerbwirkung unter den Wert von ungestrahlten Federn absinkt. Vermieden werden sollte zudem Überstrahlen. Bei zu langer Strahldauer oder zu hoher Abwurfgeschwindigkeit sind sowohl die Entstehung schuppenartiger Werkstofftrennungen als auch Spannungsrisse möglich. Die Behandlungsdauer der Metallfeder sollte deshalb so kurz gewählt werden, dass der Eigenspannungsaufbau die gewünschte Steigerung der Dauerfestigkeit erbringt.
Unter den Links finden Sie Informationen zu weiteren Oberflächenbehandlungen für Metallfedern. Eine Dauerfestigkeitsberechnung für eine Druckfeder mit verfestigter Oberfläche durch Kugelstrahlen können Sie mit dem Gutekunst-Federnberechnungsprogramm WinFSB durchführen.
Alternativ können Sie Ihre Federdaten auch direkt an uns schicken: verkauf@gutekunst-co.com.
Weiterführende Links:
Der Begriff Torsionsfeder leitet sich von dem Verb tordieren ab, was verwinden oder verdrehen bedeutet. Wie der Name also schon beschreibt, sind Torsionsfedern Federtypen, die während ihrem Einsatz eine permanente Drehbewegung durchführen. Sie bestehen aus Drähten, Bändern oder Stäben mit meist rundem Querschnitt, die an den beiden äußeren Seiten an Bauteilen befestigt sind. Diese führen gegeneinander eine Art Schwenkbewegung um die Achse der Feder aus – dies wird auch als Torsionsmoment bezeichnet. Torsionsfedern kommen vor allem bei Anwendungen zum Einsatz, bei denen ein Drehmoment erzeugt oder Rotationsenergie gesammelt werden soll.
Torsionsfedern sind vielseitig einsetzbar. Anwendungsgebiete sind unter anderem der Industrie- und Anlagenbau wie auch die Automobilbranche. Darüber hinaus werden Torsionsfedern aber auch beispielsweise in Sektional-Garagentoren verbaut.
Ihre vielfältigen Einsatzmöglichkeiten fordern unterschiedliche Ausführungen: Neben geraden Torsionsfedern, die als Stab- oder Drehstabfedern bezeichnet werden, gibt es auch Schraubendruckfedern und Schraubenzugfedern, die eine gewundene Form aufweisen.
Die Stab- oder Drehstabfeder hat einen gestreckten, stabförmigen Aufbau. Wird der Stab um seine eigene Längsachse verdreht, entsteht eine Schubspannung. Diese wächst mit dem Querschnittsradius (r) an und ist außerdem proportional zum Torsionsmoment (Mt). Im Stabquerschnitt verhält sich die Schubspannungsverteilung rotationssymmetrisch. Auch der Verdrehwinkel (φ) ist proportional zum Torsionsmoment und vergrößert sich linear mit der Stablänge.
Eingesetzt werden Drehstäbe beispielsweise als Torsionspendel in mechanischen Uhren, als Torsionsband in Drehspulmessinstrumenten sowie als Stabilisator zur Federung von Fahrzeugen.

Schraubenfedern bestehen aus Federstahldraht, der in Schraubenform gewunden ist. Unterschieden wird bei den Schraubfedern zwischen Schraubendruckfedern oder Schraubenzugfedern. Sie werden ihrer Bezeichnung entsprechend entweder zusammengepresst oder auseinandergezogen und umgangssprachlich als Druckfeder und Zugfeder benannt. Durch ihre verschiedenen Bauformen – zylindrisch, kegel- und tonnenförmig – werden sie vielseitig eingesetzt.
Im Gegensatz zu den geraden Stab- oder Drehstabfedern ist die Spannungsverteilung bei Schraubenfedern im Querschnitt nicht rotationssymmetrisch. Die Spannung der konkaven Randfasern ist erhöht und muss mit Korrekturfaktoren ausgeglichen werden. Wenn bei der Herstellung der Krümmung keine Wärmenachbehandlung erfolgt, wird die zulässige Spannung gemindert.
Die Federrate oder Federkonstante (c) beschreibt die Torsionsbeanspruchung. Sie kann mit der folgenden Formel berechnet werden:
Dabei gelten die nachstehenden Formelzeichen:
c = Federkonstante
F = belastende Kraft
f = Federweg
d = Drahtdurchmesser
D = mittlerer Windungsdurchmesser
i = Anzahl federnden Windungen
G = Schubmodul
Weiterführende Links: